
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:
 如图,在同一平面内有四个点A、B、C、D,请按要求完成下列问题.(注:此题作图不需要写画法和结论)
如图,在同一平面内有四个点A、B、C、D,请按要求完成下列问题.(注:此题作图不需要写画法和结论)查看答案和解析>>
科目:初中数学 来源: 题型:
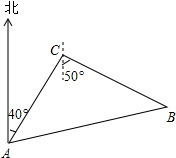 如图,某巡逻艇在A处发现北偏东40°相距9海里的C处有一艘走私船,正沿南偏东50°的方向以10海里/时的速度向我海岸行驶,巡逻艇立即以14海里/时的速度沿着直线方向追去,问需要多少时间才能追赶上该走私船?巡逻艇应该沿什么方向去追?
如图,某巡逻艇在A处发现北偏东40°相距9海里的C处有一艘走私船,正沿南偏东50°的方向以10海里/时的速度向我海岸行驶,巡逻艇立即以14海里/时的速度沿着直线方向追去,问需要多少时间才能追赶上该走私船?巡逻艇应该沿什么方向去追?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 “囧”(jiǒng)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
“囧”(jiǒng)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com