
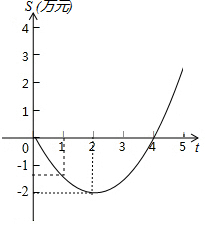 某电脑公司开发出一种软件,从研发到年初上市后,经历了从亏损到盈利的过程,如图中的图象是抛物线的一段,它刻画了该软件上市以来累积利润S(万元)与销售时间t(月)之间的函数关系(即前t个月的利润总和S与t之间的函数关系),根据图象提供的信息,解答下列问题:
某电脑公司开发出一种软件,从研发到年初上市后,经历了从亏损到盈利的过程,如图中的图象是抛物线的一段,它刻画了该软件上市以来累积利润S(万元)与销售时间t(月)之间的函数关系(即前t个月的利润总和S与t之间的函数关系),根据图象提供的信息,解答下列问题:分析 (1)根据函数图象可以直接解答本题;
(2)根据函数图象中的数据可以求得累积利润S(万元)与时间t(月)之间的函数表达式;
(3)将S=30代入(2)中的函数解析式即可解答本题;
(4)将t=6代入(2)中的函数解析式即可解答本题.
解答 解:(1)由图象可得,
该种软件上市第4个月后开始盈利;
(2)设S=a(t-2)2-2,
∵函数图象过点(0,0),
∴0=a(0-2)2-2,得a=$\frac{1}{2}$,
∴累积利润S(万元)与时间t(月)之间的函数表达式是:S=$\frac{1}{2}$(t-2)2-2;
(3)当S=30时,
30=$\frac{1}{2}$(t-2)2-2,
解得,t1=10,t2=-6(舍去),
即截止到10月末,公司累积利润达到30万元;
(4)当t=6时,
S=$\frac{1}{2}$(6-2)2-2=6,
即公司第6个月末所累积的利润是6万元.
点评 本题考查二次函数的应用、一元二次方程的应用,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用二次函数的性质和一元二次方程的相关知识解答.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
 数学活动课上,同学们正在讨论一道习题:
数学活动课上,同学们正在讨论一道习题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,CO的延长线交⊙O于点E,BA,ED的延长线交于点F.
如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,CO的延长线交⊙O于点E,BA,ED的延长线交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,点O在对角线AC上,以OA的半径的⊙O与AD、AC分别交于点E、F,且∠ACB=∠DCE.若tan∠ACB=$\frac{{\sqrt{2}}}{2}$,BC=2,则⊙O的半径为$\frac{\sqrt{6}}{4}$.
如图,在矩形ABCD中,点O在对角线AC上,以OA的半径的⊙O与AD、AC分别交于点E、F,且∠ACB=∠DCE.若tan∠ACB=$\frac{{\sqrt{2}}}{2}$,BC=2,则⊙O的半径为$\frac{\sqrt{6}}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com