
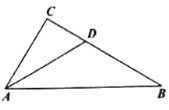
【题目】如图,∠CAB+∠ABC=90°,AD平分∠CAB,与BC边交于点D,BE平分∠ABC与AC边交于点E。
(1)依题意补全图形,并猜想∠DAB+∠EBA的度数等于__________;
(2)证明以上结论。
证明:∵ AD平分∠CAB,BE平分∠ABC,
∴∠DAB=![]() ∠CAB,
∠CAB,
∠EBA=__________.
(理由:____________________)
∵∠CAB+∠ABC=90°,
∴∠DAB+∠EBA=______×(∠______+∠______)=______。
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2;
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两车间共120人,其中甲车间人数比乙车间人数的4倍少5人.
(1)求甲、乙两车间各有多少人?
(2)若从甲、乙两车间分别抽调工人,组成丙车间研制新产品,并使甲、乙、丙三个车间的人数比为13∶4∶7,那么甲、乙两车间要分别抽调多少工人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明元旦前到文具超市用15元买了若干练习本,元旦这一天,该超市开展优惠活动,同样的练习本比元旦前便宜0.2元,小明又用20.7元钱买练习本,所买练习本的数量比上一次多50%,小明元旦前在该超市买了多少本练习本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列材料来自2006年5月衢州有关媒体的真实报道:有关部门进行民众安全感满意度调查,方法是:在全市内采用等距抽样,抽取32个小区,共960户,每户抽一名年满16周岁并能清楚表达意见的人,同时,对比前一年的调查结果,得到统计图如下: 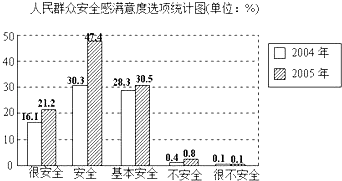
写出2005年民众安全感满意度的众数选项是;该统计图存在一个明显的错误是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量? 操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
球的颜色 | 无记号 | 有记号 | ||
红色 | 黄色 | 红色 | 黄色 | |
摸到的次数 | 18 | 28 | 2 | 2 |
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
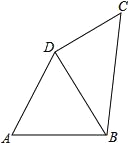
【题目】如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,四边形ABCD的周长为32.
(1)求∠BDC的度数;
(2)四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB与△OCD都是等边三角形,连接AC、BD相交于点E.
(1)求证:①△OAC≌△OBD,②∠AEB=60°;
(2)连结OE,OE是否平分∠AED?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
A.如图,在△ABC中,∠C=90°.若BD∥AE,∠DBC=20°,则∠CAE的度数是 ;
B.用科学计算器计算:![]() sin58°≈(精确到0.01).
sin58°≈(精确到0.01).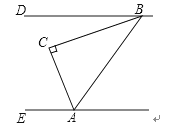
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com