练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．若二次函数y=（m-1）x2+5x+m2-3m+2的图象经过原点．则m的值等于（　　）
    A．1B．2C．1或2D．0

    分析 将原点坐标（0，0）代入二次函数解析式，列方程求m即可．

    解答 解：∵点（0，0）在抛物线y=（m-1）x2+5x+m2-3m+2上，
    ∴m2-3m+2=0，
    解得m=2或1．
    故选C．

    点评 此题考查了二次函数图象上点的坐标特征，将点的坐标代入解析式是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．如图，在平行四边形OABC中，点A在x轴上，∠AOC=60°，OC=4cm，OA=8cm，动点P从点O出发，以1cm/s的速度沿线段OA-AB运动；动点Q同时从点O出发，以1cm/s的速度沿线段OC-CB运动，其中一点先到达终点B时，另一点也随之停止运动，设运动时间为t秒．

    （1）填空：点C的坐标是（2，2$\sqrt{3}$），对角线OB的长度是4$\sqrt{7}$cm；
    （2）设△OPQ的面积为S，求S与t的函数关系式，并直接写出当t为何值时，S的值最大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．周老师在对多项式x2-7x+12进行因式分解时，先将常数项12拆成-16+28后再分组，过程如下：
    x2-7x+12=x2-7x-16+28
    =（x2-16）+（28-7x）
    =（x+4）（x-4）+7（4-x）
    =（x-4）（x+4-7）
    =（x-4）（x-3）
    请你参考上面做法分解因式：
    （1）x2+3x+2；（2）2x2+5x-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．在△ABC中，∠ABC=90°，点C在x轴正半轴上，点A在x轴负半轴上，点B在y轴正半轴上如图所示，若tan∠BAC=$\frac{1}{2}$，OB=2，求经过A、B、C点的抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：2sin230°+3cos45°•sin45°-4（tan45°-2013）0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．分解因式：
    （1）x3-2x2y+xy2；
    （2）-4a2+12ab-9b2；
    （3）-2a2x4+16a2x2-32a2；
    （4）（a2+4b2）2-16a2b2
    （5）x2-2（实数范围内分解）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．据介绍．分时电表安装后．居民峰谷分时电价分为高峰时段和低谷时段，8：00到21：00为“峰时”，21：00到次日8：00为“谷时”，和原民用电价相比，“峰时”电价上升了0.03元/KW•h，而“谷时”，电价则下降了0.22元/KW•h，有一位居民观在每天旱上用电饭煲煮稀饭，在晚上用洗衣机洗衣服，使用热水器烧水供生活用，具体使用情况如下表：
    家电名称电饭煲洗衣机热水器
    使用时间段8：00～8：2021：05～21：4520：45～21：20
    用电量/kW•h0.4 0.63.5
    电费/元0.220.18 1.425
    （1）请分别求出用电的“峰时”和“谷时”的电价是多少？并填写表中空格；
    （2）若和原民电相比，一年下来按表中值计算，分时电表安装后这位居民家中的小家电一共可以节省多少钱？（一年按365天计）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．多项式（|a|-3）x3-（a-3）x2+x+4是关于x的二次三项式，则a2-2a-3的值为12．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

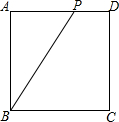    19．如图所示，正方形ABCD的边长为4cm，点P是AD边上的一个动点，则△ABP的面积S（cm2）与AP的长x（cm）之间的函数表达式为S=2x，x的取值范围是0＜x＜4．

    查看答案和解析>>

    同步练习册答案