
【题目】如图,点P是∠MON内的一点,过点P作PA⊥OM于点A,PB⊥ON于点B,且OA=OB.
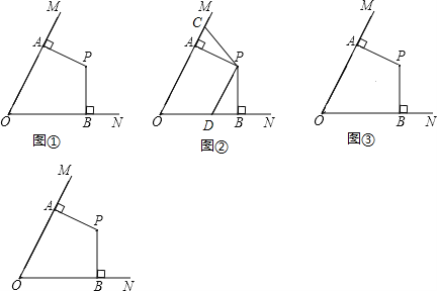
(1)求证:PA=PB;
(2)如图②,点C是射线AM上一点,点D是线段OB上一点,且∠CPD+∠MON=180°,若OC=8,OD=5.求线段OA的长.
(3)如图③,若∠MON=60°,将PB绕点P以每秒2°的速度顺时针旋转,12秒后,PA开始绕点P以每秒10°的速度顺时针旋转,PA旋转270°后停止,此时PB也随之停止旋转.旋转过程中,PA所在直线与OM所在直线的交点记为G,PB所在直线与ON所在直线的交点记为H.问PB旋转几秒时,PG=PH?
【答案】(1)见解析;(2)OA=6.5;(3)满足条件的t的值为15s或25s或37.5s.
【解析】
(1)如图1中,连接OP,证明Rt△OPA≌Rt△OPB(HL)即可解决问题.
(2)如图②中,想办法证明OC+OD=2OA即可解决问题.
(3)设点P的旋转时间为t秒.分四种情形①当0<t<12时,不存在.②当12≤t<21时,如图3-1中.③当21≤t<30时,如图3-2中.④当30≤t<39时,如图3-3中,分别求解即可解决问题.
(1)证明:如图①中,连接OP.
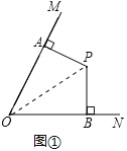
∵PA⊥OM,PB⊥ON,
∴∠OAP=∠OBP=90°,
∵OA=OB,OP=OP,
∴Rt△OPA≌Rt△OPB(HL),
∴PA=PB.
(2)如图②中,
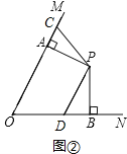
∵∠PAO=∠PBO=90°,
∴∠AOB+∠APB=180°,
∵∠CPD+∠AOB=180°,
∴∠CPD=∠APB,
∴∠APC=∠BPD,
∵PA=PB,∠PAC=∠PBD=90°,
∴△PAC≌△PBD(ASA),
∴AC=BD,
∴OC+OD=OA+AC+OB-BD=2OA=13,
∴OA=6.5.
(3)设点P的旋转时间为t秒.
①当0<t<12时,此时只有PB旋转,PA没有旋转,故不存在PG=PH.
②当PA旋转的度数为0°—90°时,时间t的取值为:12≤t<21;
∴当12≤t<21时,如图3-1中,∠APG=(10t-120)°,∠BPH=2t°,
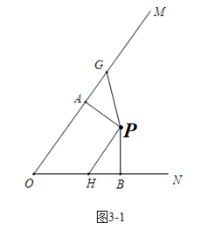
当∠APG=∠BPH时,△PAG≌△PBH,可得PG=PH,
此时10t-120=2t,
∴t=15.
③当PA旋转的度数为90°—180°时,时间t的取值为:21≤t<30,
∴当21≤t<30时,如图3-2中,∠APG=180°-∠APA′=180°-(10t-120)°=(300-10t)°,∠BPH=2t,
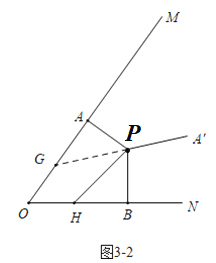
当∠APG=∠BPH时,△PAG≌△PBH,可得PG=PH,
此时300-10t=2t,
∴t=25.
④当PA旋转的度数为180°—270°时,时间t的取值为:30≤t<39;
当30≤t<39时,如图3-3中,∠APG=(10t-300)°,∠BPH=2t,
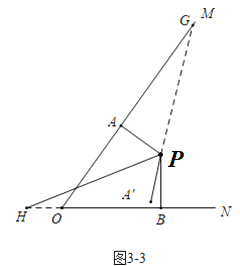
当∠APG=∠BPH时,△PAG≌△PBH,可得PG=PH,
此时10t-300=2t,
∴t=37.5;
综上所述,满足条件的t的值为15s或25s或37.5s.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
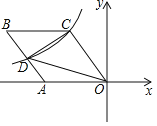
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,数![]() 所对应的点与原点的距离叫做数
所对应的点与原点的距离叫做数![]() 的绝对值,记作
的绝对值,记作![]()
提出问题:(1)点![]() 所表示的数如图所示,则
所表示的数如图所示,则![]() 两点间的距离是 ,
两点间的距离是 ,![]() 两点间的距离是_____,
两点间的距离是_____,![]() 两点间的距离是 .
两点间的距离是 .
探究结论:(2)在数轴上,若![]() 两点对应的数分别是
两点对应的数分别是![]() ,则
,则![]() ____ (用含有
____ (用含有![]() 的式子表示).
的式子表示).
拓展应用:(3)请利用.上述结论,解决下列问题:
①![]() 和
和![]() 在数轴上对应的点之间的距离为
在数轴上对应的点之间的距离为
②![]()
③满足![]() 的未知数的值为
的未知数的值为

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机动车出发前油箱内有油42L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据图回答问题:
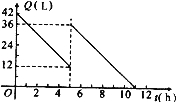
(1)机动车行驶 h后加油;
(2)加油前油箱余油量Q与行驶时间t的函数关系式是 ;
(3)中途加油 L;
(4)如果加油站距目的地还有230km,车速为40km/h,要到达目的地,油箱中的油是否够用?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
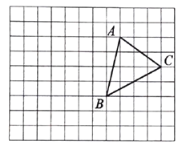
【题目】在如图所示的方格纸中,小正方形的顶点叫做格点,![]() 是一个格点三角形(即
是一个格点三角形(即![]() 的三个顶点都在格点上),根据要求回答下列问题:
的三个顶点都在格点上),根据要求回答下列问题:
![]() 画出
画出![]() 先向左平移6格,再向上平移
先向左平移6格,再向上平移![]() 格所得的
格所得的![]() ;
;
![]() 利用网格画出
利用网格画出![]() 中
中![]() 边上的高
边上的高![]() .
.
![]() 过点
过点![]() 画直线,将
画直线,将![]() 分成面积相等的两个三角形;
分成面积相等的两个三角形;
![]() 画出与
画出与![]() 有一条公共边,且与
有一条公共边,且与![]() 全等的格点三角形.
全等的格点三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
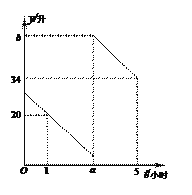
【题目】张师傅驾驶某种型号轿车从甲地去乙地,该种型号轿车每百公里油耗为10升(每行驶100公里需消耗10升汽油).途中在加油站加了一次油,加油前,根据仪表盘显示,油箱中还剩4升汽油.假设加油前轿车以80公里/小时的速度匀速行驶,加油后轿车以90公里/小时的速度匀速行驶(不计加油时间),已知油箱中剩余油量y(升)与行驶时间t(小时)之间的函数关系如图所示.
(1) 加油前,该轿车每小时消耗汔油 升;加油后,该轿车每小时消耗汔油 升;
(2)求加油前油箱剩余油量y(升)与行驶时间t(小时)之间的函数表达式;
(3)求张师傅在加油站加了多少升汽油.
查看答案和解析>>
科目:初中数学 来源: 题型:
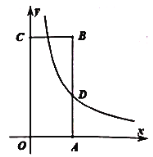
【题目】如图,矩形![]() 放置在平面直角坐标系上,点
放置在平面直角坐标系上,点![]() 分别在
分别在![]() 轴,
轴,![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的坐标是
的坐标是![]() ,其中
,其中![]() ,反比例函数y=
,反比例函数y=![]()
![]() 的图象交
的图象交![]() 交于点
交于点![]() .
.
(1)![]() _____(用
_____(用![]() 的代数式表示)
的代数式表示)
(2)设点![]() 为该反比例函数图象上的动点,且它的横坐标恰好等于
为该反比例函数图象上的动点,且它的横坐标恰好等于![]() ,连结
,连结![]() .
.
①若![]() 的面积比矩形
的面积比矩形![]() 面积多8,求
面积多8,求![]() 的值。
的值。
②现将点![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到点
得到点![]() ,若点
,若点![]() 恰好落在
恰好落在![]() 轴上,直接写出
轴上,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
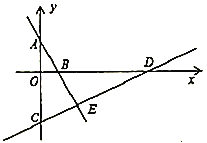
【题目】如图,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() 、与
、与![]() 轴交于点
轴交于点![]() .
.
(1)直线![]() 解析式为
解析式为![]() ,求直线
,求直线![]() 与
与![]() 交点
交点![]() 的坐标;
的坐标;
(2)四边形![]() 的面积是________;
的面积是________;
(3)求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王红有5张写着以下数字的卡片,请按要求抽出卡片,完成下列各题:![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最小,最小值是 .
(2)从中取出2张卡片,使这2张卡片数字相除商最大,最大值是 .
(3)从中取出除0以外的4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,(注:每个数字只能用一次,如:23×[1﹣(﹣2)]),请另写出一种符合要求的运算式子 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com