
 如图,在平面直角坐标系xOy中,四边形ODEF和四边形ABCD都是正方形,点F在
如图,在平面直角坐标系xOy中,四边形ODEF和四边形ABCD都是正方形,点F在分析 设OD=a,AD=b,则点E(a,a),点B(a+b,b),由反比例函数图象上点的坐标特征即可得出关于a、b的二元二次方程组,解之取a、b均为正值的解即可.
解答 解:设OD=a,AD=b,则点E(a,a),点B(a+b,b),
∵反比例函数y=$\frac{4}{x}$的图象过点B、E,
∴$\left\{\begin{array}{l}{a•a=4}\\{(a+b)•b=4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=2}\\{b=\sqrt{5}-1}\end{array}\right.$,$\left\{\begin{array}{l}{a=2}\\{b=-\sqrt{5}-1}\end{array}\right.$(舍去),$\left\{\begin{array}{l}{a=-2}\\{b=1+\sqrt{5}}\end{array}\right.$(舍去),$\left\{\begin{array}{l}{a=-2}\\{b=1-\sqrt{5}}\end{array}\right.$(舍去).
∴AB=AD=b=$\sqrt{5}$-1.
故答案为:$\sqrt{5}$-1.
点评 本题考查了反比例函数图象上点的坐标特征、正方形的性质以及解二元二次方程组,根据反比例函数图象上点的坐标特征找出关于a、b的二元二次方程组是解题的关键.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:选择题
| A. | k>1 | B. | k<1 | C. | k≥1 | D. | k≤1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
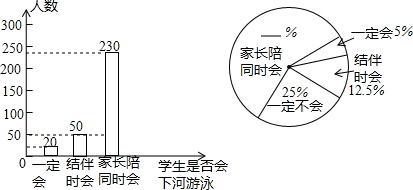
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
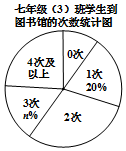 为了落实漳州市教育局关于全市中小学生每天阅读1小时的文件精神.某校对七年级(3)班全体学生一周到图书馆的次数做了调查统计,以下是调查过程中绘制的还不完整的两个统计图.请你根据统计图表中的信息,解答下列问题:
为了落实漳州市教育局关于全市中小学生每天阅读1小时的文件精神.某校对七年级(3)班全体学生一周到图书馆的次数做了调查统计,以下是调查过程中绘制的还不完整的两个统计图.请你根据统计图表中的信息,解答下列问题:| 到图书馆的 次数 | 0次 | 1次 | 2次 | 3次 | 4次及 以上 |
| 人数 | 5 | 10 | m | 8 | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
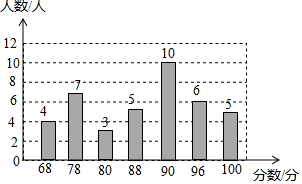 2016年合肥市初中生学业质量绿色指标综合评价在合肥12个县(市)、区312所学校进行,某校八年级根据比例被随机抽取了40名学生参与了语文、数学、英语、科学等四个科目的测试,根据这40位同学的数学成绩,绘制了如下条形统计图.
2016年合肥市初中生学业质量绿色指标综合评价在合肥12个县(市)、区312所学校进行,某校八年级根据比例被随机抽取了40名学生参与了语文、数学、英语、科学等四个科目的测试,根据这40位同学的数学成绩,绘制了如下条形统计图.| 平均成绩(分) | 中位数(分) | 众数(分) |
| 86.85 | 90 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
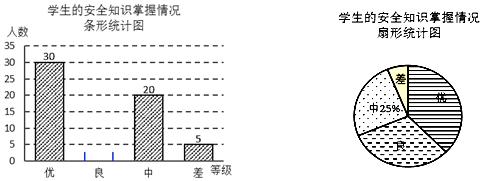
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
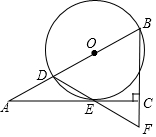 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D在AB上,以BD为直径的⊙O切AC于点E,连接DE并延长,交BC的延长线于点F.
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D在AB上,以BD为直径的⊙O切AC于点E,连接DE并延长,交BC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
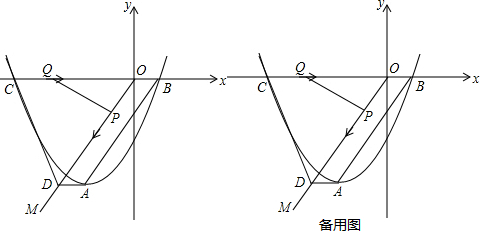
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com