
分析 由于抛物线的顶点在x轴负半轴上,那么根的判别式△=0(因为抛物线与x轴只有一个交点),且抛物线的对称轴x=-$\frac{b}{2a}$<0;联立上述两式可求得m的值.
解答 解:∵抛物线y=-2x2+2mx-$\frac{3}{4}$的顶点在x轴的负半轴上,
∴△=(2m)2-4×(-2)×(-$\frac{3}{4}$)=0,且对称轴x=-$\frac{2m}{4}$<0,
解得:m=±$\frac{\sqrt{6}}{2}$,且m>0,
∴m=$\frac{\sqrt{6}}{2}$.
点评 本题主要考查了二次函数的性质,二次函数解析式的确定、二次函数与一元二次方程的关系,以及抛物线的对称轴的求法.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,如果DE∥BC,DF∥AC,则不正确的是( )
如图,在△ABC中,如果DE∥BC,DF∥AC,则不正确的是( )| A. | $\frac{AE}{EC}$=$\frac{CF}{FB}$ | B. | $\frac{BF}{BC}$=$\frac{DF}{AC}$ | C. | $\frac{AC}{AE}$=$\frac{AB}{AC}$ | D. | $\frac{AD}{FC}$=$\frac{AB}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根 | |
| B. | 如果方程M有两根符号相同,那么方程N的两根符号也相同 | |
| C. | 如果5是方程M的一个根,那么$\frac{1}{5}$是方程N的一个根 | |
| D. | 如果方程M和方程N有一个相同的根,那么这个根必是x=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
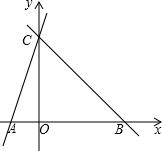 如图,直线y=kx+k交x轴、y轴分别于A,C,直线BC过点C交x轴于B,OC=3OA,∠CBA=45°.
如图,直线y=kx+k交x轴、y轴分别于A,C,直线BC过点C交x轴于B,OC=3OA,∠CBA=45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com