
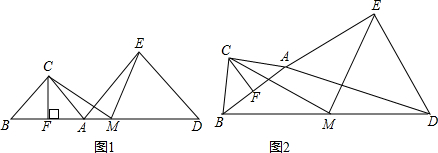
分析 (1)利用勾股定理可分别求得AB和AD的长,再由中点的定义可求得BM和BF的长,从而可求得FM;
(2)过点E作EN⊥BD交点N,由中点的定义可求得FN=BM,从而可求得CF=MN,同理可得到EN=FM,则可证明△CFM≌△MNE,可证得结论;
(3)取AD的中点H,连接EH、MH、MF,利用三角形的中位线可得MF=$\frac{1}{2}$AD=EH,HM=$\frac{1}{2}$AB=CF,可证明△CFM≌△MHE,再利用平行线的性质可证得∠CME=∠CFA=90°,可得出CM和EM的数量关系和位置关系.
解答 解:
(1)∵AC=BC=1,AE=AD=2,∠ACB=∠AED=90°,
∴AB=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,AD=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴BD=AB+AD+3$\sqrt{2}$,
∵CF⊥AB,
∴F为AB中点,且M为BD中点,
∴BF=$\frac{1}{2}$AB=$\frac{\sqrt{2}}{2}$,BM=$\frac{1}{2}$BD=$\frac{3\sqrt{2}}{2}$,
∴FM=BM-BF=$\frac{3\sqrt{2}}{2}$-$\frac{\sqrt{2}}{2}$=$\sqrt{2}$;
(2)如图1,过E作EN⊥BD,交BD于点N,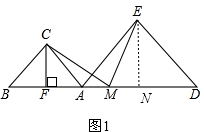
∵F为AB中点,N为AD中点,
∴FN=FA+AN=$\frac{1}{2}$(AB+AD)=$\frac{1}{2}$BD,
∵M为BD中点,
∴BM=$\frac{1}{2}$BD,
∴FN=BM,即BF+FM=FM+MN,
∴BF=MN,
又CF=BF,
∴CF=MN,
同理可得EN=FM,且∠CFM=∠MNE=90°,
∴在△CFM和△MNE中
$\left\{\begin{array}{l}{CF=MN}\\{∠CFM=∠MNE}\\{FM=NE}\end{array}\right.$
∴△CFM≌△MNE(SAS),
∴CM=EM;
(3)如图2,过E作EH⊥AD于点H,则H为AD中点,设AB与CM交于点O,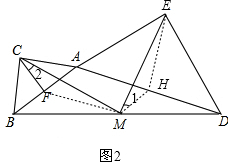
∵M为BD中点,
∴MH∥AB且MH=$\frac{1}{2}$AB,
∵CF⊥AB,
∴F为AB中点,
∴AF=CF=$\frac{1}{2}$AB,
∴CF=MH,
同理可得MF=HE,
∵MH∥AB,MF∥AD,
∴∠MHA+∠BAH=∠MFA+∠BAH=180°,
∴∠MHA=∠MFA,
∵CF⊥AB,EH⊥AD,
∴∠CFA=∠EHA=90°,
∴∠CFM=∠MHE,
在△CFM和△MHE中
$\left\{\begin{array}{l}{CF=MH}\\{∠CFM=∠MHE}\\{MF=HE}\end{array}\right.$
∴△CFM≌△MHE(SAS),
∴CM=EM,∠1=∠2,
∵MH∥AB,
∴∠BOM=∠OMH,即∠2+∠CFA=∠1+∠CME,
∴∠CME=∠CFA=90°,
∴CM⊥EM,
综上可知CE=EM且CM⊥EM.
点评 本题为三角形的综合应用,涉及知识点有等腰直角三角形的性质、勾股定理、全等三角形的判定和性质、三角形中位线定理等.在(2)、(3)中构造三角形,找到三角形全等的条件是解题的关键.本题考查知识点较多,综合性很强,难度较大.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.97×109 | B. | 197×108 | C. | 1.97×1010 | D. | 19.7×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com