
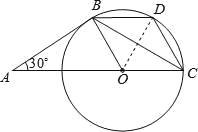
【题目】如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30°,D为![]() 的中点.
的中点.
(1)求证:AB=BC;
(2)求证:四边形BOCD是菱形.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由AB是⊙O的切线,∠A=30°,易求得∠OCB的度数,继而可得∠A=∠OCB=30°,又由等角对等边,证得AB=BC;
(2)首先连接OD,易证得△BOD与△COD是等边三角形,可得OB=BD=OC=CD,即可证得四边形BOCD是菱形.
试题解析:(1)∵AB是⊙O的切线,
∴OB⊥AB,
∵∠A=30°,
∴∠AOB=60°,
∵OB=OC,
∴∠OCB=∠OBC=![]() ∠AOB=30°,
∠AOB=30°,
∴∠A=∠OCB,
∴AB=BC;
(2)连接OD,
∵∠AOB=60°,
∴∠BOC=120°,
∵D为![]() 的中点,
的中点,
∴![]() ,∠BOD=∠COD=60°,
,∠BOD=∠COD=60°,
∵OB=OD=OC,
∴△BOD与△COD是等边三角形,
∴OB=BD=OC=CD,
∴四边形BOCD是菱形.


科目:初中数学 来源: 题型:
【题目】某商店购进一批进价为20元/件的日用商品,第一个月,按进价提高50%的价格出售,售出400件,第二个月,商店准备在不低于原售价的基础上进行加价销售,根据销售经验,提高销售单价会导致销售量的减少.销售量y(件)与销售单价x(元)的关系如图所示.
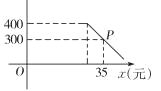
(1)图中点P所表示的实际意义是 ;销售单价每提高1元时,销售量相应减少 件;
(2)请直接写出y与x之间的函数表达式: ;自变量x的取值范围为 ;
(3)第二个月的销售单价定为多少元时,可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若 二 次 函 数 y ax bx c 的 图 象 与 x 轴 交 于 A 和 B 两 点 , 顶 点 为 C , 且b 4ac 4 ,则 ACB 的度数为()
A. 120° B. 90° C. 60° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在 ABC 中, ACB 90, B 60, BC 2 ,MON 30.
(1)如图 1, MON 的边 MO ⊥ AB ,边 ON 过点 C ,求 AO 的长;
(2)如图 2,将图 1 中的 MON 向右平移,MON 的两边分别与 ABC 的边 AC 、BC
相交于点 E 、 F ,连接 EF ,若 OEF 是直角三角形,求 AO 的长;
(3)在(2)的条件下,MON 与 ABC 重叠部分面积是否存在最大值,若存在,求出 最大值,若不存在,请说明理由.
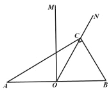
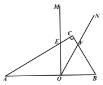
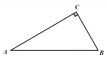
图 1 图 2 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,AO⊥BC于点O,点F是线段AO上的点(与A,O不重合),∠EAF=90°,AE=AF,连接FE,FC,BE,BF.
(1)求证:BE=BF;
(2)如图②,若将△AEF绕点A旋转,使边AF在∠BAC的内部,延长CF交AB于点G,交BE于点K.求证:△AGC∽△KGB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com