
【题目】△ABC内接于圆O,且AB=AC,圆O的半径等于6cm,O点到BC距离等于2cm,则AB长为_____cm.
【答案】4![]() 或4
或4![]() .
.
【解析】
首先注意到,由于不知道![]() 是锐角还是钝角,所以造成圆心在三角形内部和外部两种情况. ①当圆心在三角形内部时, 连接AO并延长交BC于D点,根据垂径定理在
是锐角还是钝角,所以造成圆心在三角形内部和外部两种情况. ①当圆心在三角形内部时, 连接AO并延长交BC于D点,根据垂径定理在![]() 中先求
中先求![]() 的长度,再在
的长度,再在![]() 根据勾股定理求
根据勾股定理求![]() 即可. ②当圆心在三角形外部时,连接AO交BC于D点,先求
即可. ②当圆心在三角形外部时,连接AO交BC于D点,先求![]() 的长度, 再在
的长度, 再在![]() 根据勾股定理求
根据勾股定理求![]() 即可.
即可.
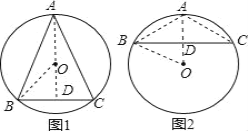
解:①当圆心在三角形内部时(如图1),
连接AO并延长交BC于D点,
∵AB=AC,
∴AD⊥BC,
依题意,得AO=BO=6,OD=2,
由勾股定理,得AB2﹣AD2=BO2﹣OD2=BD2,
AB2﹣(6+2)2=62﹣22,解得AB=4![]() ;
;
②当圆心在三角形外部时(如图2),
连接AO交BC于D点,
∵AB=AC,
∴AD⊥BC,
依题意,得AO=BO=6,OD=2,
由勾股定理,得AB2﹣AD2=BO2﹣OD2=BD2,
AB2﹣(6﹣2)2=62﹣22,解得AB=4![]() .
.
∴AB=4![]() cm或4
cm或4![]() cm.
cm.
故本题答案为:4![]() 或4
或4![]() .
.


科目:初中数学 来源: 题型:
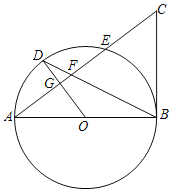
【题目】如图所示,AB是⊙O的直径,G为弦AE的中点,OG的延长线交⊙O于点D,连接BD交AE于点F,延长AE至点C,使得FC=BC,连接BC.
(1)求证:BC是⊙O的切线;
(2)⊙O的半径为10,tanA=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
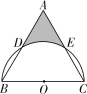
【题目】如图,等边△ABC的边长为4,以BC为直径的半圆O交AB于点D,交AC于点E,则图中阴影部分的面积是( )
A.2![]() -
-![]() B.2
B.2![]() -
-![]()
C.4![]() +-
+-![]() D.4
D.4![]() -
-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】11月21日,“中国流动科技馆”榆林市第二轮巡展启动仪式在榆阳区青少年校外活动中心盛大举行,此次巡展以“体验科学”为主题.榆林市某中学举行了“科普知识”竞赛,为了解此次“科普知识”竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并制作出如下的不完整的统计表和统计图,如图所示.请根据图表信息解答以下问题.
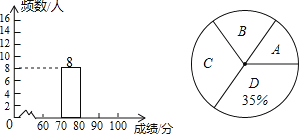

(1)表中a= ;一共抽取了 个参赛学生的成绩;
(2)补全频数分布直方图;
(3)计算扇形统计图中“B”与“C”对应的圆心角度数;
(4)若成绩在80分以上(包括80分)的为“优”等,所抽取学生成绩为“优”的占所抽取学生的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A、C的坐标分别为(4,6)、(5,4),且AB平行于x轴,将矩形ABCD向左平移,得到矩形A′B′C′D′.若点A′、C′同时落在函数![]() 的图象上,则k的值为( )
的图象上,则k的值为( )
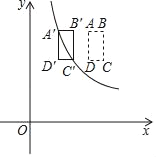
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》.意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB、AD中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=( )

A.1.2 里B.1.5 里C.1.05 里D.1.02 里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的学习材料:
我们知道,一般情况下式子![]() 与“
与“![]() ”是不相等的(m,n均为整数),但当m,n取某些特定整数时,可以使这两个式子相等,我们把使“
”是不相等的(m,n均为整数),但当m,n取某些特定整数时,可以使这两个式子相等,我们把使“![]() =
=![]() ”成立的数对“m,n”叫做“好数对”,记作[m,n],例如,当m=n=0时,有
”成立的数对“m,n”叫做“好数对”,记作[m,n],例如,当m=n=0时,有![]() =
=![]() 成立,则数对“0,0”就是一对“好数对”,记作[0,0]
成立,则数对“0,0”就是一对“好数对”,记作[0,0]
解答下列问题:
(1)通过计算,判断数对“3,4”是否是“好数对”;
(2)求“好数对”[x,﹣32]中x的值;
(3)请再写出一对上述未出现的“好数对”[ , ];
(4)对于“好数对[a,b],如果a=9k(k为整数),则b= (用含k的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线![]() 的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
①2b﹣c=2;②a=![]() ;③ac=b﹣1;④
;③ac=b﹣1;④![]() >0
>0
其中正确的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
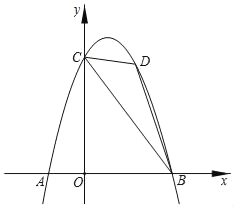
【题目】如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0)两点,与y轴交于点C,点D是抛物线上一个动点,设点D的横坐标为m(1<m<4)连接BC,DB,DC.
(1)求抛物线的函数解析式;
(2)△BCD的面积是否存在最大值,若存在,求此时点D的坐标;若不存在,说明理由;
(3)在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形.若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com