
 如图,在平行四边形ABCD中,BC=6cm,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形.求:
如图,在平行四边形ABCD中,BC=6cm,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形.求:分析 (1)首先根据等边三角形的性质可得DF=DC=FC,∠D=60°,根据折叠的性质,∠BCA=∠ECA,再利用平行四边形的性质证明∠DAC=30°,∠ACD=90°,利用直角三角形30°角所对的边等于斜边的一半可得CD长,进而可得AB的长;
(2)由(1)可知,∠ACD=90°,由AB∥CD,推出∠BAC=∠ACD=90°,再利用勾股定理求出AC即可;
(3)利用三角函数值计算出AC,然后根据三角形的中线平分三角形的面积可得S△ACF=$\frac{1}{2}$S△ACD,进而可得答案.
解答 解:(1)∵△CDE为等边三角形,
∴DE=DC=EC,∠D=∠CED=60°,
根据折叠的性质,∠BCA=∠B′CA,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=6cm,AB=CD,
∴∠EAC=∠BCA,
∴∠EAC=∠ECA
∴EA=EC,
∴∠DAC=30°,
∴∠ACD=90°,
∴CD=$\frac{1}{2}$AD=3cm,
∵AB=3cm;
(2)结论:AC⊥BB′,
理由:由(1)可知,∠ACD=90°,
∵AB∥CD,
∴∠BAC=∠ACD=90°,
∴AC⊥BB′,
在Rt△ABC中,AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$.
(3)∵CD=3cm,∠ACD=90°,∠DAC=30°,
∴AC=3 $\sqrt{3}$cm,
∴S△ACE=$\frac{1}{2}$S△ACD=$\frac{1}{4}$×AC•CD=$\frac{1}{4}$×3×3 $\sqrt{3}$=$\frac{9\sqrt{3}}{4}$(cm2).
点评 此题主要考查了平行四边形的性质、直角三角形的性质以及翻折变换,关键是掌握平行四边形的对边平行且相等,直角三角形30°角所对的边等于斜边的一半.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
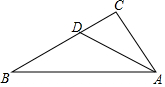 如图所示,△ABC中,∠C=90°,AD平分∠BAC,AB=7cm,CD=3cm,则△ABD的面积是$\frac{21}{2}$cm2.
如图所示,△ABC中,∠C=90°,AD平分∠BAC,AB=7cm,CD=3cm,则△ABD的面积是$\frac{21}{2}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
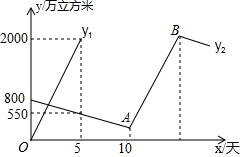 因南方旱情严重,乙水库的蓄水量以每天相同的速度持续减少,为缓解旱情,北方甲水库立即以管道运输的方式给予支援,如图是乙水库的蓄水量y1(单位:万立方米)关于时间x(单位:天)的函数图象和甲水库输水量y1(单位:万立方米)关于时间x(0≤x≤5)的函数图象,在单位时间内、甲水库的放水量与乙水库的进水量相同(水在排放、接收以及输送过程中的损耗不计),通过分析图象解答下列问题:
因南方旱情严重,乙水库的蓄水量以每天相同的速度持续减少,为缓解旱情,北方甲水库立即以管道运输的方式给予支援,如图是乙水库的蓄水量y1(单位:万立方米)关于时间x(单位:天)的函数图象和甲水库输水量y1(单位:万立方米)关于时间x(0≤x≤5)的函数图象,在单位时间内、甲水库的放水量与乙水库的进水量相同(水在排放、接收以及输送过程中的损耗不计),通过分析图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com