
分析 (1)设一只A型节能灯节能灯的售价为m元,一只B型节能灯节能灯的售价为n元,根据“1只A型节能灯和3只B型节能灯共需12元,3只A型节能灯和2只B型节能灯共需29元”即可得出关于m、n的二元一次方程组,解之即可得出结论;
(2)设购进B型节能灯x只,总费用为y元,则购进A型节能灯(50-x)只,根据A型节能灯的数量不多于B型节能灯数量的3倍即可得出关于x的一元一次不等式,解之即可得出x的取值范围,再根据总价=单价×数量即可得出y关于x的函数关系式,根据一次函数的性质即可解决最值问题.
解答 解:(1)设一只A型节能灯节能灯的售价为m元,一只B型节能灯节能灯的售价为n元,
根据题意得:$\left\{\begin{array}{l}{m+3n=12}\\{3m+2n=29}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=9}\\{n=1}\end{array}\right.$.
答:一只A型节能灯节能灯的售价为9元,一只B型节能灯节能灯的售价为1元.
(2)设购进B型节能灯x只,总费用为y元,则购进A型节能灯(50-x)只,
根据题意得:50-x≤3x,
解得:x≥$\frac{25}{2}$,
∵x为正整数,
∴13≤x<50.
∵y=9(50-x)+x=-8x+450,-8<0,
∴当x=49时,y取最小值,最小值为58.
答:当购买A型节能灯1只、B型节能灯49只时,总费用最低,最低费用为58元.
点评 本题考查了二元一次方程组的应用、一次函数的性质以及一元一次不等式的应用,解题的关键是:(1)根据A、B型节能灯的购买数量以及总费用列出关于m、n的二元一次方程组;(2)根据总价=单价×数量找出y关于x的函数关系式.


科目:初中数学 来源: 题型:解答题
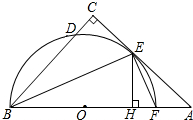 如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
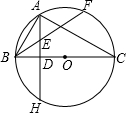 如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为$\widehat{BF}$的中点,BF交AD于点E,且BE•EF=32,AD=6
如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为$\widehat{BF}$的中点,BF交AD于点E,且BE•EF=32,AD=6查看答案和解析>>
科目:初中数学 来源: 题型:解答题
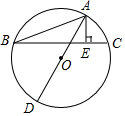 如图,A,B,C为⊙O上的点,AD为⊙O的直径,AE⊥BC于E,AB=5,BE=$\sqrt{21}$,CE=$\sqrt{5}$,求AD的长.
如图,A,B,C为⊙O上的点,AD为⊙O的直径,AE⊥BC于E,AB=5,BE=$\sqrt{21}$,CE=$\sqrt{5}$,求AD的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
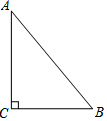 如图是一块直角三角形的绿地,量得直角边BC为6cm,AC为8cm,现在要将原绿地扩充后成三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后的等腰三角形绿地的周长.
如图是一块直角三角形的绿地,量得直角边BC为6cm,AC为8cm,现在要将原绿地扩充后成三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后的等腰三角形绿地的周长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com