
【题目】如图,平面直角坐标系中有点A(0,1)、B(![]() ,0).
,0).
连接AB,以A为圆心,以AB为半径画弧,交y轴于点P1;
连接BP1,以B为圆心,以BP1为半径画弧,交x轴于点P2;
连接P1P2,以P1为圆心,以P1P2为半径画弧,交y轴于点P3;
按照这样的方式不断在坐标轴上确定点Pn的位置,那么点P6的坐标是_____.
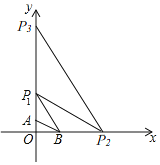
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图1,在△ABC中,把AB绕点A按顺时针方向旋转α(0°<α<180°)得到AB′,把AC绕点A按逆时针方向旋转β得到AC′,连接B′C′,当α+β=180°时,我们称△AB′C′是△ABC的“旋补三角形”,△AB′C′边B′C′上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
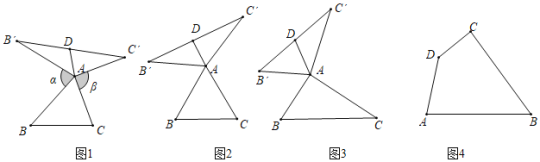
(1)特例感知:在图2、图3中,△AB′C′是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD=______BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为______.
(2)精确作图:如图4,已知在四边形ABCD内部存在点P,使得△PDC是△PAB的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点P(要求:保留作图痕迹,不写作法和证明)
(3)猜想论证:在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
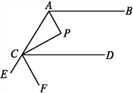
【题目】如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.
(1)用α表示∠ACP;
(2)求证:AB∥CD;
(3)若AP∥CF,求证:FC平分∠DCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017甘肃省天水市)△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年中国北京世界园艺博览会于4月28日晚在北京·延庆隆重开幕,本届世园会主题为“绿色生活、美丽家园”.自开园以来,世园会迎来了世界各国游客进园参观.据统计,仅五一小长假前来世园会打卡的游客就总计约32.7万人次.其中中国馆也是非常受欢迎的场馆.据调查,中国馆5月1日游览人数约为4万人,5月3日游览人数约为9万人,若5月1日到5月3日游客人数的日增长率相同,求中国馆这两天游客人数的日平均增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)把方程(3x+2)(x-3)=2x-6,化为一般形式,并写出它的二次项系数、一次项系数和常数项.
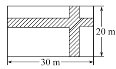
(2)在宽为20m、长为30m的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551m2,则修建的路宽应为多少?(只列方程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com