
【题目】如果向东走50米记作+50米,那么﹣50米表示( )
A.向西走50米
B.向南走50米
C.向北走50米
D.向东走50米
科目:初中数学 来源: 题型:
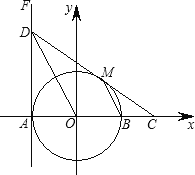
【题目】如图,在平面直角坐标系xOy中,⊙O交x轴于A、B两点,直线FA⊥x 轴于点A,点D在FA上,且DO平行⊙O的弦MB,连DM并延长交x轴于点C.
(1)判断直线DC与⊙O的位置关系,并给出证明;
(2)设点D的坐标为(﹣2,4),试求MC的长及直线DC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
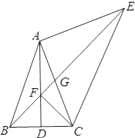
【题目】在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
(1)若∠BAC=40°,求∠AEB的度数;
(2)求证:∠AEB=∠ACF;
(3)求证:EF2+BF2=2AC2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,在距离O点80米的A处有一所学校,当重型运输卡车P沿道路ON方向行驶时,距离卡车50米范围内都会受到卡车噪声的影响.
(1)学校A是否受到卡车噪声的影响?为什么?
(2)假如学校A会受到噪声的影响,若卡车以每小时18km的速度行驶,求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
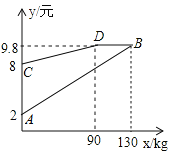
【题目】2015年全球葵花籽产量约为4200万吨,比2014年上涨2.1%,某企业加工并销售葵花籽,假设销售量与加工量相等,在图中,线段AB、折线CDB分别表示葵花籽每千克的加工成本y1(元)、销售价y2(元)与产量x(kg)之间的函数关系;
(1)请你解释图中点B的横坐标、纵坐标的实际意义;
(2)求线段AB所表示的y1与x之间的函数解析式;
(3)当0<x≤90时,求该葵花籽的产量为多少时,该企业获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人;已知36座客车每辆租金400元,42座客车每辆租金440元.
(1)该校初三年级共有多少人参加春游?
(2)请你帮该校设计一种最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+ax+a-2=0
(1)若该方程有一个实数根为1,求a的值及方程的另一实根.
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
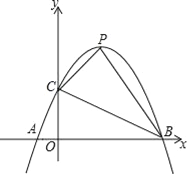
【题目】已知,如图,抛物线y=﹣x2+ax+b与x轴从左至右交于A、B两点,与y轴正半轴交于点C.设∠OCB=α,∠OCA=β,且tanα﹣tanβ=2,OC2=OAOB.
(1)△ABC是否为直角三角形?若是,请给出证明;若不是,请说明理由;
(2)求抛物线的解析式;
(3)若抛物线的顶点为P,求四边形ABPC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com