分析:连接OA、OB、OC、OD.构建等腰直角三角形AOD、等边三角形COD,然后利用它们的性质及三角形内角和来求α=180°-∠CAB-∠OBA-∠OBD=75°.
解答: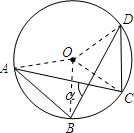
解:连接OA、OB、OC、OD,
∵OA=OB=OC=OD=1,AB=
,CD=1,
∴OA
2+OB
2=AB
2,
∴△AOB是等腰直角三角形,△COD是等边三角形,
∴∠OAB=∠OBA=45°,∠ODC=∠OCD=60°,
∵∠CDB=∠CAB,∠ODB=∠OBD,
∴α=180°-∠CAB-∠OBA-∠OBD=180°-∠OBA-(∠CDB+∠ODB)=180°-45°-60°=75°.
故答案是:75°.
点评:本题考查了勾股定理的逆定理,圆周角的性质,等边三角形的性质以及三角形的内角和定理.本题通过作辅助线“连接OA、OB、OC、OD”构建等腰直角三角形AOD、等边三角形COD,然后利用它们的性质解答问题.

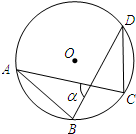 如图⊙O的半径为1,弦AB,CD的长度分别为
如图⊙O的半径为1,弦AB,CD的长度分别为 解:连接OA、OB、OC、OD,
解:连接OA、OB、OC、OD,

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案