
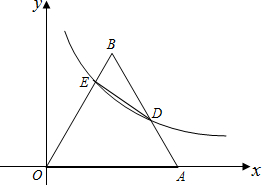
 如图,等边△ABO在平面直角坐标系中,点A的坐标为(4,0),反比例函数y=$\frac{k}{x}$(x>0,k≠0)的图象经过AB的中点D,交OB于E.
如图,等边△ABO在平面直角坐标系中,点A的坐标为(4,0),反比例函数y=$\frac{k}{x}$(x>0,k≠0)的图象经过AB的中点D,交OB于E.分析 (1)过点B作BC⊥x轴于点C,则OC=AC=2,根据等边三角形的性质求得OC和BC的长,得到点B的坐标,然后根据待定系数法求得直线OB的解析式;根据中点的性质求得AB的中点D的坐标,代入y=$\frac{k}{x}$,即可求得k的值;
(2)先将直线OB的解析式与反比例函数的解析式联立求出E点坐标,求出BE、BD的长,再作EF⊥BD于F,求出EF,然后根据三角形面积公式求解即可.
解答 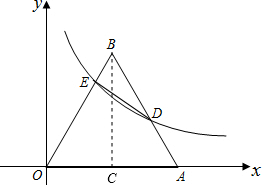 解:(1)过点B作BC⊥x轴于点C,
解:(1)过点B作BC⊥x轴于点C,
∵△ABO是等边三角形,点A的坐标为(4,0),
∴OC=AC=2.
由勾股定理得:BC=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴B(2,2$\sqrt{3}$),
设直线OB的函数解析式为y=mx,则2$\sqrt{3}$=2m,
∴m=$\sqrt{3}$.
∴直线OB的函数解析式为y=$\sqrt{3}$x;
∵D为AB的中点,
∴D(3,$\sqrt{3}$),
∴k=3$\sqrt{3}$; (2)将y=$\sqrt{3}$x代入y=$\frac{3\sqrt{3}}{x}$,得$\sqrt{3}$x=$\frac{3\sqrt{3}}{x}$,
(2)将y=$\sqrt{3}$x代入y=$\frac{3\sqrt{3}}{x}$,得$\sqrt{3}$x=$\frac{3\sqrt{3}}{x}$,
解得x=±$\sqrt{3}$(负值舍去),
则E($\sqrt{3}$,3),
∵B(2,2$\sqrt{3}$),D(3,$\sqrt{3}$),
∴BE=$\sqrt{(2-\sqrt{3})^{2}+(2\sqrt{3}-3)^{2}}$=4-2$\sqrt{3}$,BD=$\frac{1}{2}$AB=$\frac{1}{2}$OA=2.
如图,作EF⊥BD于F,则EF=BE•sin∠B=(4-2$\sqrt{3}$)×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$-3,
∴△BDE的面积=$\frac{1}{2}$BD•EF=$\frac{1}{2}$×2×(2$\sqrt{3}$-3)=2$\sqrt{3}$-3.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了等边三角形的性质,勾股定理,三角形的面积.利用待定系数法求出函数的解析式是解题的关键.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
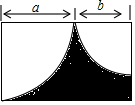 如图所示,用含a、b字母的代数式表示图中阴影部分的面积为${a}^{2}+ab-\frac{π{a}^{2}}{4}-\frac{π{b}^{2}}{4}$.
如图所示,用含a、b字母的代数式表示图中阴影部分的面积为${a}^{2}+ab-\frac{π{a}^{2}}{4}-\frac{π{b}^{2}}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,有两条公路OM,ON相交成30°角.沿公路OM方向离O点80米处有一所学校A,当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
如图,有两条公路OM,ON相交成30°角.沿公路OM方向离O点80米处有一所学校A,当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com