
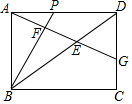
 如图,长方形ABCD中,P是AD上一动点,连接BP,过点A作BP的垂线,垂足为F,交BD于点E,交CD于点G.
如图,长方形ABCD中,P是AD上一动点,连接BP,过点A作BP的垂线,垂足为F,交BD于点E,交CD于点G.分析 (1)根据BP⊥AG,AB=AD,四边形ABCD是矩形,运用AAS判定△ABP≌△DAG,即可得出AG=BP;
(2)根据△ABP≌△DAG,得出AP=DG,再根据AP=$\frac{1}{2}$AD,即可得到DG=$\frac{1}{2}$AD=$\frac{1}{2}$AB,再根据AB∥CD,判定△DGE∽△BAE,最后根据相似三角形的性质,得出$\frac{DE}{BE}$=$\frac{DG}{BA}$=$\frac{1}{2}$;
(3)设AP=a,则AD=2AP=2a,AB=3AD=6a,根据△ABP∽△DAG,即可求得$\frac{AP}{GD}$=$\frac{AB}{DA}$,得出DG=$\frac{1}{3}$a,再根据△DGE∽△BAE,运用相似三角形的性质,得出$\frac{DE}{BE}$=$\frac{DG}{BA}$=$\frac{\frac{1}{3}a}{6a}$=$\frac{1}{18}$即可.
解答  解:(1)如图,∵BP⊥AG,∠BAD=90°,
解:(1)如图,∵BP⊥AG,∠BAD=90°,
∴∠ABF+∠BAF=90°,∠BAF+∠DAG=90°,
∴∠ABF=∠DAG,
在△ABP和△DAG中,
$\left\{\begin{array}{l}{∠BAP=∠ADG=90°}\\{∠ABF=∠DAG}\\{AB=DA}\end{array}\right.$,
∴△ABP≌△DAG(AAS),
∴AG=BP;
(2)∵△ABP≌△DAG,
∴AP=DG,
∵AP=$\frac{1}{2}$AD,
∴DG=$\frac{1}{2}$AD=$\frac{1}{2}$AB,
∵AB∥CD,
∴△DGE∽△BAE,
∴$\frac{DE}{BE}$=$\frac{DG}{BA}$=$\frac{1}{2}$;
(3)设AP=a,则AD=2AP=2a,AB=3AD=6a,
∵BP⊥AG,∠BAD=90°,
∴∠ABF+∠BAF=90°,∠BAF+∠DAG=90°,
∴∠ABF=∠DAG,
又∵∠BAP=∠ADG,
∴△ABP∽△DAG,
∴$\frac{AP}{GD}$=$\frac{AB}{DA}$,即$\frac{a}{DG}$=$\frac{6a}{2a}$=3,
∴DG=$\frac{1}{3}$a,
∵AB∥GD,
∴△DGE∽△BAE,
∴$\frac{DE}{BE}$=$\frac{DG}{BA}$=$\frac{\frac{1}{3}a}{6a}$=$\frac{1}{18}$.
故答案为:$\frac{1}{18}$.
点评 本题属于相似形综合题,主要考查了相似三角形的判定与性质,全等三角形的殴打与性质的综合应用,解决问题的关键是根据相似三角形的对应边相等,以及相似三角形的对应边成比例进行推导计算.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
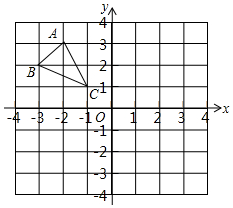 如图,在平面直角坐标中,△ABC各顶点都在小方格的顶点上.
如图,在平面直角坐标中,△ABC各顶点都在小方格的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | |
| 甲种车辆数单位(辆) | 2 | 5 |
| 乙种车辆数单位(辆) | 3 | 6 |
| 累计运货数单位(吨) | 15.5 | 35 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com