Question

【题目】已知：如图，正方形的边长为，，分别平分正方形的两个外角，且满足，连接，，．

求证：；

求的度数．

Answer 1

【答案】（1）详见解析；（2）135°.

【解析】

（1）如图（3）由条件可以得出∠BMA=∠3，∠ABM=∠ADN=135°，就可以得出△ABM∽△NDA，利用相似三角形的性质就可以得出BMDN=36；

（2）由△ABM∽△NDA，可以得出BM：DA=AB：ND，再由正方形的性质通过等量代换就可以得出△BCM∽△DNC．利用角的关系和圆周角的度数就可以求出结论；

（3）将△AND绕点A顺时针旋转90°得到△ABF，连接MF，证明△ABF≌△ADN．利用边角的关系得出△BMF是直角三角形，由勾股定理就可以得出结论．

证明：

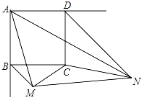
∵，分别平分正方形的两个外角，

∴，

∵四边形是正方形，

∴，，

∴，

∵，

，∵，

∴，

∴，

∴，

∴．

∵，

∴，∵，

∴，

∴，

∵，

∴，

∴．