
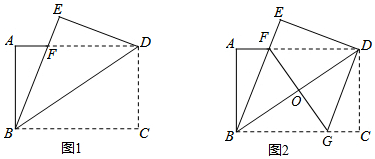
分析 (1)根据两直线平行内错角相等及折叠特性判断;
(2)①根据已知矩形性质及第一问证得邻边相等判断;
②根据折叠特性设未知边,构造勾股定理列方程求解.
解答 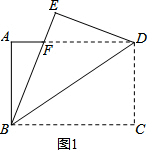 (1)证明:如图1,根据折叠,∠DBC=∠DBE,
(1)证明:如图1,根据折叠,∠DBC=∠DBE,
又AD∥BC,
∴∠DBC=∠ADB,
∴∠DBE=∠ADB,
∴DF=BF,
∴△BDF是等腰三角形;
(2)①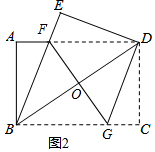 ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴AD∥BC,
∴FD∥BG,
又∵DG∥BE,
∴四边形BFDG是平行四边形,
∵DF=BF,
∴四边形BFDG是菱形;
②∵AB=6,AD=8,
∴BD=10.
∴OB=$\frac{1}{2}$BD=5.
假设DF=BF=x,∴AF=AD-DF=8-x.
∴在直角△ABF中,AB2+AF2=BF2,即62+(8-x)2=x2,
解得x=$\frac{25}{4}$,
即BF=$\frac{25}{4}$,
∴FO=$\sqrt{B{F}^{2}-O{B}^{2}}$=$\sqrt{(\frac{25}{4})^{2}-{5}^{2}}$=$\frac{15}{4}$,
∴FG=2FO=$\frac{15}{2}$.
点评 此题考查了四边形综合题,结合矩形的性质、菱形的判定和性质、勾股定理解答,考查了翻折不变性,综合性较强,是一道好题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
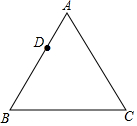 如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
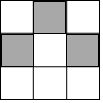 如图,在“3×3”网格中,有3个涂成黑色的小方格.若再从余下的6个小方格中随机选取1个涂成黑色,则完成的图案为轴对称图案的概率是$\frac{1}{3}$.
如图,在“3×3”网格中,有3个涂成黑色的小方格.若再从余下的6个小方格中随机选取1个涂成黑色,则完成的图案为轴对称图案的概率是$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
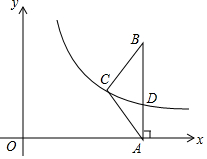 如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=$\frac{5}{2}$.
如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=$\frac{5}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
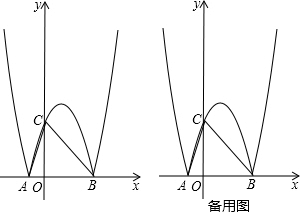
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com