
【题目】某中学为数学实验“先行示范校”,一数学活动小组带上高度为1.5m的测角仪BC,对建筑物AO进行测量高度的综合实践活动,如图,在BC处测得直立于地面的AO顶点A的仰角为30°,然后前进40m至DE处,测得顶点A的仰角为75°.
(1)求∠CAE的度数;
(2)求AE的长(结果保留根号);
(3)求建筑物AO的高度(精确到个位,参考数据:![]() ,
,![]() ).
).

【答案】(1)45°;(2)![]() ;(3)29.
;(3)29.
【解析】
(1)先根据测得顶点A的仰角为75°,求出∠AEC的度数进而求∠CAE的度数;
(2)延长CE交AO于点G,过点E作EF⊥AC垂足为F.解直角三角形即可得到结论;
(3)根据题干条件直接解直角三角形即可得到结论.
解:(1)由测得顶点A的仰角为75°,可知∠AEC=180°-75°=105°,又顶点A的仰角为30°即∠ACE=30°,所以∠CAE=180°-105°-30°=45°;
(2)延长CE交AO于点G,过点E作EF⊥AC垂足为F.
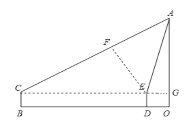
由题意可知:∠ACG=30°,∠AEG=75°,CE=40,
∴∠EAC=∠AEG-∠ACG=45°,
∵EF=CE×Sin∠FCE=20,
∴AE=![]() ,
,
∴AE的长度为![]() m;;
m;;
(3)∵CF=CE×cos∠FCE=![]() ,AF=EF=20,
,AF=EF=20,
∴AC=CF+AF=![]() +20,
+20,
∴AG=AC×Sin∠ACG=![]() ,
,
∴AO=AG+GO=![]() +1.5=
+1.5=![]() ≈29,
≈29,
∴高度AO约为29m.


科目:初中数学 来源: 题型:
【题目】定义:方程cx2+bx+a=0是一元二次方程ax2+bx+c=0的倒方程.
(1)已知x=2是x2+2x+c=0的倒方程的解,求c的值;
(2)若一元二次方程ax2﹣2x+c=0无解,求证:它的倒方程也一定无解;
(3)一元二次方程ax2﹣2x+c=0(a≠c)与它的倒方程只有一个公共解,它的倒方程只有一个解,求a和c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李宁准备完成题目;解二元一次方程组![]() ,发现系数“□”印刷不清楚.
,发现系数“□”印刷不清楚.
(1)他把“□”猜成3,请你解二元一次方程组![]() ;
;
(2)张老师说:“你猜错了”,我看到该题标准答案的结果x、y是一对相反数,通过计算说明原题中“□”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,点
,点![]() 是线段
是线段![]() 的一个三等分点,以点
的一个三等分点,以点![]() 为圆心,
为圆心,![]() 为半径的圆交
为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]()
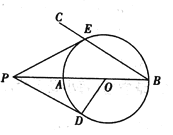
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)点![]() 为
为![]() 上的一动点,连接
上的一动点,连接![]() .
.
①当![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②当![]() 时,四边形
时,四边形![]() 是矩形.
是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
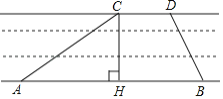
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使用家用燃气灶烧开同一壶水所需的燃气量![]() (单位:
(单位:![]() )与旋钮的旋转角度
)与旋钮的旋转角度![]() (单位:度)(
(单位:度)(![]() )近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度
)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度![]() 与燃气量
与燃气量![]() 的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
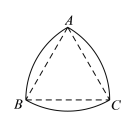
【题目】我们研究过的图形中,圆的任何一对平行切线的距离总是相等的,所以圆是“等宽曲线”.除了圆以外,还有一些几何图形也是“等宽曲线”,如勒洛三角形(如图![]() ),它是分别以等边三角形的每个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧,三段圆弧围成的曲边三角形. 图
),它是分别以等边三角形的每个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧,三段圆弧围成的曲边三角形. 图![]() 是等宽的勒洛三角形和圆形滚木的截面图.
是等宽的勒洛三角形和圆形滚木的截面图.

图![]() 图
图![]()
有如下四个结论:
①勒洛三角形是中心对称图形
②图![]() 中,点
中,点![]() 到
到![]() 上任意一点的距离都相等
上任意一点的距离都相等
③图![]() 中,勒洛三角形的周长与圆的周长相等
中,勒洛三角形的周长与圆的周长相等
④使用截面是勒洛三角形的滚木来搬运东西,会发生上下抖动
上述结论中,所有正确结论的序号是( )
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
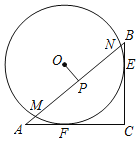
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3.直径为5的⊙O分别与AC、BC相切于点F、E,与AB交于点M、N,过点O作OP⊥MN于P,则OP的长为( )
A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com