
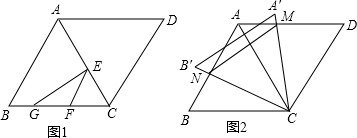
分析 (1)利用t表示出BG和CF,然后根据BG=FC即可列方程求解;
(2)分成0<x≤6和6<t≤12两种情况,即E在AC上和在AD上两种情况进行讨论,利用等腰三角形的面积公式和相似三角形的性质即可求解;
(3)证明△ACM≌△BCN,则AN+AM=AD,当AC⊥MN时,MN最短,求得MN即可求得三角形的周长.
解答 解:(1)设运动时间是t.
∵EF∥AB,
∴∠EFC=∠B=60°,
又∵∠ACB=60°,
∴△EFC是等边三角形.
∴CF=CE=t.
在直角△CEG中,CG=$\frac{EC}{cos∠ECG}$=2t.
则BG=BC-CG=6-2t.
根据题意得:t=6-2t,
解得:t=2.
故答案是:2;
(2)当0<x≤6时,如图①,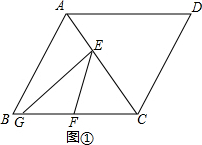
S△EFC=$\frac{\sqrt{3}{t}^{2}}{4}$,
则S=S△EFC=$\frac{\sqrt{3}}{4}$t2;
当6<t≤12时,如图②.过M作MP⊥AD于点P,交BC于点N.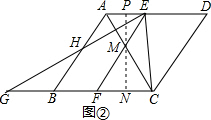
∵EF∥CD,AD∥BC,
∴四边形EFCD是平行四边形,
∴CF=DE=12-t,AE=t-6.
∵AE∥BC,
∴△AME∽△CMF,
∴$\frac{PM}{MN}$=$\frac{AE}{CF}$=$\frac{t-6}{12-t}$,
又∵PN=MN+MP=AB•sin60°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$.
∴MN=-$\frac{\sqrt{3}}{2}$t+6$\sqrt{3}$,
则S=$\frac{1}{2}$CF•MN=$\frac{1}{2}$(12-t)(-$\frac{\sqrt{3}}{2}$t+6$\sqrt{3}$),
则S=$\frac{\sqrt{3}}{4}$t2-6$\sqrt{3}$t+36$\sqrt{3}$;
(3)∵∠A'CB'=60°即∠NCA+∠ACM=60°,
又∵∠BNC+∠NCA=∠ACB=60°,
∴∠BCN=∠ACM,
在△ACM和△BCN中,
$\left\{\begin{array}{l}{∠MAC=∠B}\\{AC=BC}\\{∠BCN=∠ACM}\end{array}\right.$,
∴△ACM≌△BCN(ASA),
∴BN=AM,
同理,AN=DM,
则AN+AM=AD=6.
当AC⊥MN时,MN最短.此时CN⊥AB,
则AN=$\frac{1}{2}$AB=3.
则MN=2AN•sin60°=2×3×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
则△AMN的周长的最小值是:6+3$\sqrt{3}$.
点评 本题是函数与相似三角形的判定与性质以及全等三角形的判定与性质的综合题,主要考查了分类讨论的思想,正确利用t表示出MN的长度是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图A、B、C是△ABC三个顶点
如图A、B、C是△ABC三个顶点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
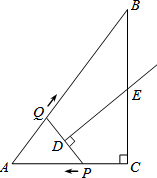 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P,Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P,Q同时出发,当点Q到达点B时停止运动,点P也随之停止运动.设点P,Q运动的时间是t秒(t>0).
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P,Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P,Q同时出发,当点Q到达点B时停止运动,点P也随之停止运动.设点P,Q运动的时间是t秒(t>0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
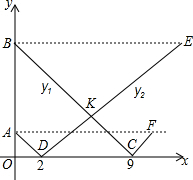 甲,乙两地相距630千米,客车从甲地出发向乙地匀速行驶,同时货车从乙地出发,向甲地匀速行驶,在甲乙两地间有一中途站P,货车的速度是客车的$\frac{3}{4}$,客、货车到P站的距离分别为y1、y2(千米),它们与行驶时间x(小时)之间的函数关系如图所示,则下列结论:①客车的速度为60千米/小时;②货车的速度为45千米/小时;③两车相遇的时间为6小时;④点E的坐标为(14,540).说法正确的个数有( )个.
甲,乙两地相距630千米,客车从甲地出发向乙地匀速行驶,同时货车从乙地出发,向甲地匀速行驶,在甲乙两地间有一中途站P,货车的速度是客车的$\frac{3}{4}$,客、货车到P站的距离分别为y1、y2(千米),它们与行驶时间x(小时)之间的函数关系如图所示,则下列结论:①客车的速度为60千米/小时;②货车的速度为45千米/小时;③两车相遇的时间为6小时;④点E的坐标为(14,540).说法正确的个数有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com