

分析 (1)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC-∠NOC求出即可;
(2)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC-∠NOC求出即可;
(3)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC-∠NOC求出即可.
解答 解:(1)如图1,∵∠AOB=90°,∠BOC=60°,
∴∠AOC=90°+60°=150°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=$\frac{1}{2}$∠AOC=75°,∠NOC=$\frac{1}{2}$∠BOC=30°
∴∠MON=∠MOC-∠NOC=45°.
(2)如图2,∠MON=$\frac{1}{2}$α,
理由是:∵∠AOB=α,∠BOC=60°,
∴∠AOC=α+60°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=$\frac{1}{2}$∠AOC=$\frac{1}{2}$α+30°,∠NOC=$\frac{1}{2}$∠BOC=30°
∴∠MON=∠MOC-∠NOC=($\frac{1}{2}$α+30°)-30°=$\frac{1}{2}$α.
(3)如图3,∠MON=$\frac{1}{2}$α,与β的大小无关.
理由:∵∠AOB=α,∠BOC=β,
∴∠AOC=α+β.
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠MOC=$\frac{1}{2}$∠AOC=$\frac{1}{2}$(α+β),
∠NOC=$\frac{1}{2}$∠BOC=$\frac{1}{2}$β,
∴∠AON=∠AOC-∠NOC=α+β-$\frac{1}{2}$β=α+$\frac{1}{2}$β.
∴∠MON=∠MOC-∠NOC
=$\frac{1}{2}$(α+β)-$\frac{1}{2}$β=$\frac{1}{2}$α
即∠MON=$\frac{1}{2}$α.
点评 本题考查了角平分线定义和角的有关计算,关键是求出∠AOC、∠MOC、∠NOC的度数和得出∠MON=∠MOC-∠NOC.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:解答题
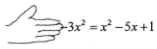 老师在黑板上书写一个正确的演算过程,随后用手掌捂住了一个二次三项式.形式如下:
老师在黑板上书写一个正确的演算过程,随后用手掌捂住了一个二次三项式.形式如下:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 32与23 | B. | (-2)2与-22 | C. | -(-2)与|-2| | D. | ($\frac{2}{3}$)2与$\frac{{2}^{2}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k≤-6 | B. | k≥-6或k≠0 | C. | k>-6且k≠0 | D. | k≥-6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com