
【题目】定义:直线![]() 与直线
与直线![]() 互为“友好直线”,如:直线
互为“友好直线”,如:直线![]() 与
与![]() 互为“友好直线”.
互为“友好直线”.
(1)点![]() 在直线
在直线![]() 的“友好直线”上,则
的“友好直线”上,则![]() ________.
________.
(2)直线![]() 上的点
上的点![]() 又是它的“友好直线”上的点,求点
又是它的“友好直线”上的点,求点![]() 的坐标;
的坐标;
(3)对于直线![]() 上的任意一点
上的任意一点![]() ,都有点
,都有点![]() 在它的“友好直线”上,求直线
在它的“友好直线”上,求直线![]() 的解析式.
的解析式.
【答案】(1)![]() ;(2)M(1,7);(3)y=x-
;(2)M(1,7);(3)y=x-![]() .
.
【解析】
(1)由“友好直线”可得直线y=-x+4的“友好直线”,代入可得m的值;
(2)先表示直线y=4x+3的“友好直线”,再分别代入列方程组可得M的坐标;
(3)先表示直线y=ax+b的“友好直线”,并将点M和N分别代入可得方程组,得:(2b+2a-1)m=-a-2b,
根据对于任意一点M(m,n)等式均成立,则![]() ,可得结论.
,可得结论.
(1)由题意得:直线y=-x+4的“友好直线”是:y=4x-1,
把(m,2)代入y=4x-1中,得:4m-1=2,
m=![]() ,
,
故答案为:![]() ;
;
(2)由题意知,y=4x+3的“友好直线”是y=3x+4,
又∵点M(m,n)是直线y=4x+3上的点,又是它的“友好直线”上的点,
∴![]() ,
,
∴解得![]() ,
,
∴点M(1,7);
(3)∵点M(m,n)是直线y=ax+b上的任意一点,
∴am+b=n①,
∵点N(2m,m-2n)是直线y=ax+b的“友好直线”上的一点,
即N(2m,m-2n)在直线y=bx+a上
∴2bm+a=m-2n②,
将①代入②得,
2bm+a=m-2(am+b),
整理得:2bm+2am-m=-a-2b,
∴(2b+2a-1)m=-a-2b,
∵对于任意一点M(m,n)等式均成立,
∴![]() ,
,
解得 ,
,
∴y=x-![]() .
.


科目:初中数学 来源: 题型:
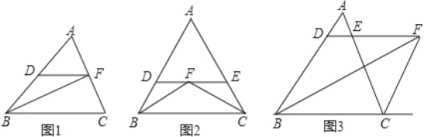
【题目】(1)如图 1,在△ABC 中,∠ABC 的平分线 BF 交 AC 于 F, 过点 F 作 DF∥BC, 求证:BD=DF.
(2)如图 2,在△ABC 中,∠ABC 的平分线 BF 与∠ACB 的平分线 CF 相交于 F,过点 F 作 DE∥BC,交直线 AB 于点 D,交直线 AC 于点 E.那么 BD,CE,DE 之间存在什么关系?并证明这种关系.
(3)如图 3,在△ABC 中,∠ABC 的平分线 BF 与∠ACB 的外角平分线 CF 相交于 F,过点 F 作 DE∥BC,交直线 AB 于点D,交直线 AC 于点 E.那么 BD,CE,DE 之间存在什么关系?请写出你的猜想.(不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
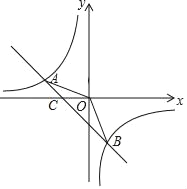
【题目】已知如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于A、B两点,A点坐标是(﹣2,1),B点坐标(1,n);
的图象相交于A、B两点,A点坐标是(﹣2,1),B点坐标(1,n);
(1)求出k,b,m,n的值;
(2)求△AOB的面积;
(3)直接写出一次函数的函数值大于反比例函数的函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
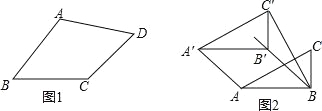
(1)如图 1,在四边形 ABCD 中,添加一个条件使得四边形 ABCD 是“等邻边四边形”.请写出你添加的一个条件.
(2)小红猜想:对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗?请说明理由.
(3)如图 2,小红作了一个Rt△ABC,其中∠ABC=90°,AB=2,BC=1,并将 Rt△ABC 沿∠ABC 的平分线 BB′方向平移得到△A′B′C′,连结 AA′, BC′.小红要使得平移后的四边形 ABC′A′是“等邻边四边形”,应平移多少距离(即线段 B′B 的长)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 请画出△ABC关于原点对称的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
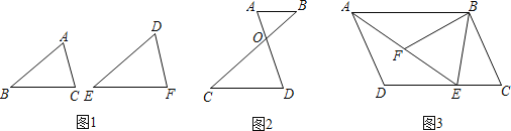
【题目】 先阅读下面的材料,再解答下面的问题:如果两个三角形的形状相同,则称这两个三角形相似.如图1,△ABC与△DEF形状相同,则称△ABC与△DEF相似,记作△ABC∽△DEF.那么,如何说明两个三角形相似呢?我们可以用“两角分别相等的三角形相似”加以说明.用数学语言表示为:
如图1:在△ABC与△DEF中,∵∠A=∠D,∠B=∠E,∴△ABC∽△DEF.
请你利用上述定理解决下面的问题:
(1)下列说法:①有一个角为50°的两个等腰三角形相似;②有一个角为100°的两个等腰三角形相似;③有一个锐角相等的两个直角三角形相似;④两个等边三角形相似.其中正确的是______(填序号);
(2)如图2,已知AB∥CD,AD与BC相交于点O,试说明△ABO∽△DCO;
(3)如图3,在平行四边形ABCD中,E是DC上一点,连接AE.F为AE上一点,且∠BFE=∠C,求证:△ABF∽△EAD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市政规划出一块矩形土地用于某项目开发,其中![]()
![]() ,设计分区如图所示,
,设计分区如图所示,![]() 为矩形内一点,作
为矩形内一点,作![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,
,![]() 过点
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,其中丙区域用于主建筑区,其余各区域均用于不同种类绿化.
,其中丙区域用于主建筑区,其余各区域均用于不同种类绿化.
![]() 若点
若点![]() 是
是![]() 的中点,求
的中点,求![]() 的长;
的长;
![]() 要求绿化占地面积不小于
要求绿化占地面积不小于![]() ,规定乙区域面积为
,规定乙区域面积为![]()
①若将甲区域设计成正方形形状,能否达到设计绿化要求?请说明理由;
②若主建筑丙区域不低于乙区域面积的![]() ,则
,则![]() 的最大值为
的最大值为 ![]() (请直接写出答案)
(请直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
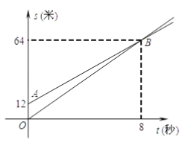
【题目】如图,![]() 分别表示两名同学沿着同一路线运动的一次函数图象,图中
分别表示两名同学沿着同一路线运动的一次函数图象,图中![]() 和
和![]() 分别表示运动路程和时间,已知甲的速度比乙快.有下列结论:
分别表示运动路程和时间,已知甲的速度比乙快.有下列结论:
①射线![]() 表示甲的运动路程与时间的函数关系
表示甲的运动路程与时间的函数关系
②甲出发时,乙已经在甲前面12米;
③8秒后,甲超过了乙;
④64秒时,甲追上了乙
其中,正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com