
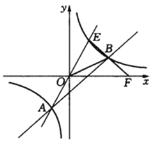
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于点A、E,AB交双曲线于另一点B(
交于点A、E,AB交双曲线于另一点B(![]() ,
,![]() ),连接EB并延长交x轴于点F.
),连接EB并延长交x轴于点F.
(1)![]() ;
;
(2)求直线AB的解析式;
(3)求△EOF的面积;
(4)若点P为坐标平面内一点,且以A,B,E,P为顶点的四边形是平行四边形,请直接写出点P的坐标.
【答案】(1)2;(2)y=x-2;(3)12;(4)(-4,-2)或(0,-6)或(8,10)
【解析】
(1)把B(![]() ,
,![]() )代入反比例函数
)代入反比例函数![]() 即可求出m的值;
即可求出m的值;
(2)联立直线y=2x与反比例函数![]() 即可求出A,E坐标,然后用待定系数法确定直线AB的关系式;
即可求出A,E坐标,然后用待定系数法确定直线AB的关系式;
(3)先用待定系数法求出EB的解析式,再令y=0,得出F的坐标,最后用三角形的面积公式求出△EOF的面积;
(4)分类讨论:分别以AB,BE,AE为对角线求对应的P的坐标.
(1)∵点B(2m,m)在反比例函数![]() 上,
上,
∴2m·m=8,解得m=±2,而m>0,
∴m=2
(2)m=2,则点B的坐标为(4,2)
联立解析式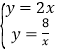 得
得![]() 或
或![]()
∴点A坐标为(-2,-4),E点坐标为(2,4)
设直线AB的解析式为y=k1x+b1,
把A(-2,-4),B(4,2)代入得:-2k1+b1=-4,4k1+b1=2,
解方程组得k1=1, b1=-2,
∴直线AB的解析式为y=x-2;
(3)设直线EB的解析式为y=k2x+b2,
把E(2,4),B(4,2)代入可得2k2+b2=4,4k2+b2=2,解得k2=-1,b2=6,
∴直线EB的解析式为y=-x+6,
令y=0,解得x=6,故F(6,0)
∴S△EOF=![]() =12
=12
(4)①以AB为对角线时,由A(-2,-4),B(4,2)求出中点O坐标为(1,-1),故E(2,4)关于中点O(1,-1)的对称点P为(0,-6);
②以BE为对角线时,由E(2,4),B(4,2)求出中点O’坐标为(3,3),故A(-2,-4)关于中点O’(3,3)的对称点P为(8,10);
③以AE为对角线时,由A(-2,-4),E(2,4)求出中点O’坐标为(0,0),故B(4,2)关于中点O’(0,0)的对称点P为(-4,-2);
故满足条件的点P的坐标为(-4,-2)或(0,-6)或(8,10)


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
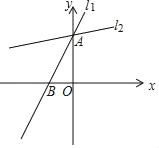
【题目】如图,已知直线l1:y=2x+4与y轴交于A点,与x轴交于点B,经过A点的直线l2与直线l1所夹的锐角为45°.
(1)过点B作CB⊥AB,交l2于C,求点C的坐标.
(2)求l2的函数解析式.
(3)在直线l1上存在点M,直线l2上存在点N,使得点A、O、M、N四点组成的四边形是平行四边形,请直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.

(1)∠1与∠2有什么关系,为什么?
(2)BE与DF有什么关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
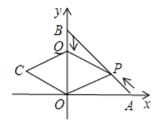
【题目】如图,A,B两点的坐标分别为(6,0),(0,6),点P从点A出发,沿AB方向以每秒![]() 个单位的速度向终点B运动;同时动点Q从点B出发沿BO方向以每秒1个单位的速度向终点Q运动,将△PQO沿BO翻折,点P的对应点为点C,若四边形QPOC为菱形,则点C的坐标为________.
个单位的速度向终点B运动;同时动点Q从点B出发沿BO方向以每秒1个单位的速度向终点Q运动,将△PQO沿BO翻折,点P的对应点为点C,若四边形QPOC为菱形,则点C的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
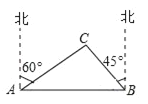
【题目】某市在新农村改造工程中需要修建一段东西方向全长1000米的道路(记作AB).已知C点周围350米范围内有一电力设施区域.在A处测得C在A的北偏东60°方向上,在B处测得C在B的北偏西45°方向上.(![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
(1)道路AB是否穿过电力设施区域?为什么?
(2)在施工250米后,为了尽量减少施工对城市交通所造成的影响,加快了施工进度,实际工作效率变成了原计划工作效率的1.5倍,结果提前5天完成了修路任务,则原计划每天修路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.

(1)求证:DE⊥BE;
(2)如果OE⊥CD,求证:BD·CE=CD·DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:
①AH=DF; ②∠AEF=45°; ③S四边形EFHG=S△DEF+S△AGH,
其中正确的结论有_____________________.(填正确的序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com