
 如图中,高BD与CE交于O点,若∠BAC=72°,则∠DOE的度数( )
如图中,高BD与CE交于O点,若∠BAC=72°,则∠DOE的度数( )

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源:2011-2012学年江苏无锡阳山中学八年级下学期期中数学试卷(带解析) 题型:解答题
如图,在△ABC中,高BD、CE相交于点O.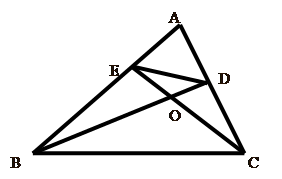
【小题1】试说明: ;
;
【小题2】试说明:△AED∽△ACB
【小题3】试说明:△DOE与△COB相似。(本题满分6分)
查看答案和解析>>
科目:初中数学 来源:2012年北师大版初中数学七年级下5.1认识三角形练习卷(解析版) 题型:选择题
如图中,高BD与CE交于O点,若∠BAC=72°,则∠DOE的度数( )

A.72° B.18° C.108° D.162°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com