
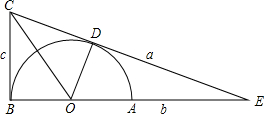
 选用适当的数,设计出计算半圆O的半径r的一种方案:
选用适当的数,设计出计算半圆O的半径r的一种方案:| a2-b2 |
| 2b |
| a2-b2 |
| 2b |
| ||
| 2 |
-b+
| ||
| 4 |
c
| ||
| a+2c |


科目:初中数学 来源: 题型:
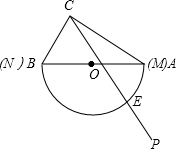 为O),现有射线CP绕点C从CA的位置开始按顺时针方向以每秒2度的速度旋转到CB位置,在旋转过程中,射线CP与量角器的半圆弧交于E.
为O),现有射线CP绕点C从CA的位置开始按顺时针方向以每秒2度的速度旋转到CB位置,在旋转过程中,射线CP与量角器的半圆弧交于E.查看答案和解析>>
科目:初中数学 来源: 题型:
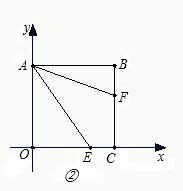
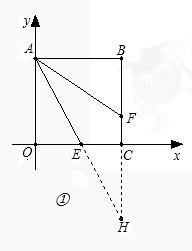 边上,且∠OAE=∠FAE
边上,且∠OAE=∠FAE| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•武汉模拟)如图,AB为⊙O的直径,AM和BN是它的两条切线,E为⊙O的半圆弧上一动点(不与A、B重合),过点E的直线分别交射线AM、BN于D、C两点,且CB=CE.
(2012•武汉模拟)如图,AB为⊙O的直径,AM和BN是它的两条切线,E为⊙O的半圆弧上一动点(不与A、B重合),过点E的直线分别交射线AM、BN于D、C两点,且CB=CE.
| ||
| 2 |
| AH |
| CH |
查看答案和解析>>
科目:初中数学 来源: 题型:
 我们新定义一种三角形:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
我们新定义一种三角形:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.查看答案和解析>>
科目:初中数学 来源: 题型:
 到CB方向,在旋转过程中,射线CP与量角器的半圆弧交于E.
到CB方向,在旋转过程中,射线CP与量角器的半圆弧交于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com