
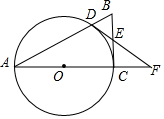
 如图,在Rt△ACB中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
如图,在Rt△ACB中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.分析 (1)连接OD、CD,由AC为⊙O的直径知△BCD是直角三角形,结合E为BC的中点知∠CDE=∠DCE,由∠ODC=∠OCD且∠OCD+∠DCE=90°可得答案;
(2)设⊙O的半径为r,由OD2+DF2=OF2,即r2+42=(r+2)2可得r=3,即可得出答案.
解答 解:(1)如图,连接OD、CD,
∵AC为⊙O的直径,
∴△BCD是直角三角形,
∵E为BC的中点,
∴BE=CE=DE,
∴∠CDE=∠DCE,
∵OD=OC,
∴∠ODC=∠OCD,
∵∠ACB=90°,
∴∠OCD+∠DCE=90°,
∴∠ODC+∠CDE=90°,即OD⊥DE,
∴DE是⊙O的切线;
(2)设⊙O的半径为r,
∵∠ODF=90°,
∴OD2+DF2=OF2,即r2+42=(r+2)2,
解得:r=3,
∴⊙O的直径为6.
点评 本题主要考查切线的判定与圆周角定理、直角三角形的性质及勾股定理,熟练掌握切线的判定与圆周角定理是解题的关键.


科目:初中数学 来源: 题型:解答题
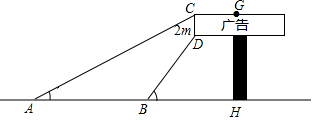 数学兴趣小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点共线,请根据以上数据计算GH的长($\sqrt{3}≈1.73$,要求结果精确得到0.1m)
数学兴趣小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点共线,请根据以上数据计算GH的长($\sqrt{3}≈1.73$,要求结果精确得到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
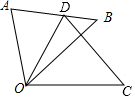 如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠B的度数是( )
如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠B的度数是( )| A. | 40° | B. | 35° | C. | 30° | D. | 15° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
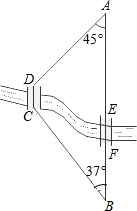 如图所示,A,B两地之间有一条河,原来从A地到B地需要经过桥DC,沿折线A⇒D⇒C⇒B到达.现在新建了一座同样长的桥EF,可直接沿直线AB从A地到达B地.已知BC=10km,∠A=45°,∠B=37°,桥DC和AB平行,则现在从A地到B地可比原来少走多少路程(结果精确到0.1km.参考数据:$\sqrt{2}$≈1.41,sin37°≈0.60,cos37°≈0.80)
如图所示,A,B两地之间有一条河,原来从A地到B地需要经过桥DC,沿折线A⇒D⇒C⇒B到达.现在新建了一座同样长的桥EF,可直接沿直线AB从A地到达B地.已知BC=10km,∠A=45°,∠B=37°,桥DC和AB平行,则现在从A地到B地可比原来少走多少路程(结果精确到0.1km.参考数据:$\sqrt{2}$≈1.41,sin37°≈0.60,cos37°≈0.80)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是$\frac{\sqrt{3}}{18}$.
如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是$\frac{\sqrt{3}}{18}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 部门 | 人数 | 每人所创年利润(单位:万元) |
| A | 1 | 10 |
| B | 3 | 8 |
| C | 7 | 5 |
| D | 4 | 3 |
| A. | 10,5 | B. | 7,8 | C. | 5,6.5 | D. | 5,5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com