

 ,点D在线段CA的延长线上,且AD=AB,若反比例函数
,点D在线段CA的延长线上,且AD=AB,若反比例函数 的图象经过点D,求k的值.
的图象经过点D,求k的值.
 。
。 ,∴∠OBA=∠1。
,∴∠OBA=∠1。 的图象经过点D,∴k=14×6=84。
的图象经过点D,∴k=14×6=84。
 ,即
,即


科目:初中数学 来源:不详 题型:解答题
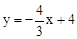 的图象与x轴、y轴分别相交于点A、B.P是射线BO上的一个动点(点P不与点B重合),过点P作PC⊥AB,垂足为C,在射线CA上截取CD=CP,连接PD.设BP=t.
的图象与x轴、y轴分别相交于点A、B.P是射线BO上的一个动点(点P不与点B重合),过点P作PC⊥AB,垂足为C,在射线CA上截取CD=CP,连接PD.设BP=t.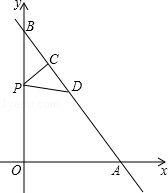
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,第8天时,雨雪停止附近的胜利农场前来支援,合作6天,完成了兴化农场所有的收割任务.图1是机械收割的亩数y1(亩)和人工收割的亩数y2(亩)与时间x(天)之间的函数图象.图2是剩余的农作物的亩数w(亩)与时间x天之间的函数图象,请结合图象回答下列问题.
,第8天时,雨雪停止附近的胜利农场前来支援,合作6天,完成了兴化农场所有的收割任务.图1是机械收割的亩数y1(亩)和人工收割的亩数y2(亩)与时间x(天)之间的函数图象.图2是剩余的农作物的亩数w(亩)与时间x天之间的函数图象,请结合图象回答下列问题.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 的图像与反比例函数
的图像与反比例函数 的图像交于二、四象限的A、B两点,与x轴交于C点。已知A(-2,m),B(n,-2),
的图像交于二、四象限的A、B两点,与x轴交于C点。已知A(-2,m),B(n,-2), ,则此一次函数的解析式为 .
,则此一次函数的解析式为 .
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过400元 | 售价打九折 |
| 超过400元 | 售价打八折 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 上一点,则点B与其对应点B′间的距离为
上一点,则点B与其对应点B′间的距离为
A. | B.3 | C.4 | D.5 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com