
| A. | 2x2-5x-4=0 | B. | 7t2-5t+2=0 | C. | x(x+1)=3 | D. | 3y2+25=10$\sqrt{3}$y |
分析 根据方程的系数结合根的判别式,逐一分析四个选项中方程根的判别式△的正负,由此即可得出结论.
解答 解:A、∵在方程2x2-5x-4=0中,△=(-5)2-4×2×(-4)=57>0,
∴方程2x2-5x-4=0有两个不相等的实数根;
B、∵在方程7t2-5t+2=0中,△=(-5)2-4×7×2=-31<0,
∴方程7t2-5t+2=0没有实数根.
C、原方程可变形为x2+x-3=0,
∵△=12-4×1×(-3)=13>0,
∴方程x(x+1)=3有两个不相等的实数根;
D、原方程整理得:3y2-10$\sqrt{3}$y+25=0,
∵△=$(-10\sqrt{3})^{2}$-4×3×25=0,
∴方程3y2+25=10$\sqrt{3}$y有两个相等的实数根.
故选B.
点评 本题考查了根的判别式,熟练掌握“当△<0时,方程无实数根”是解题的关键.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
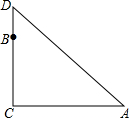 如图,在一棵树CD的10m高处B有两只猴子,其中一只猴子爬下树走到离树20m处的池塘的A处,另一只爬到树顶D后直接跃到A处,距离以直线计算.如果两只猴子所经过的距离相等,请问这棵树有多高?
如图,在一棵树CD的10m高处B有两只猴子,其中一只猴子爬下树走到离树20m处的池塘的A处,另一只爬到树顶D后直接跃到A处,距离以直线计算.如果两只猴子所经过的距离相等,请问这棵树有多高?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
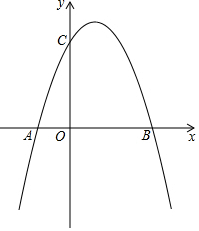 如图,抛物线y=ax2+bx+c(a≠0)与x轴相交于A(-1,0),B(3,0),与y轴交于点C(0,3).
如图,抛物线y=ax2+bx+c(a≠0)与x轴相交于A(-1,0),B(3,0),与y轴交于点C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
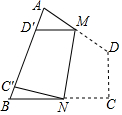 如图,四边形纸片ABCD中,∠A=75°,∠B=65°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=80°.
如图,四边形纸片ABCD中,∠A=75°,∠B=65°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=80°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
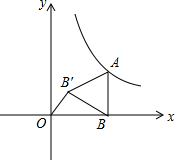 如图,点B在x的正半轴上,且BA⊥OB于点B,将线段BA绕点B逆时针旋转60°到BB′的位置,且点B′的坐标为(1,$\sqrt{3}$).若反比例函数y=$\frac{k}{x}$(x>0)的图象经过A点,则k=8$\sqrt{3}$.
如图,点B在x的正半轴上,且BA⊥OB于点B,将线段BA绕点B逆时针旋转60°到BB′的位置,且点B′的坐标为(1,$\sqrt{3}$).若反比例函数y=$\frac{k}{x}$(x>0)的图象经过A点,则k=8$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{12}{3x}$=$\frac{12}{x}$$-\frac{1}{2}$ | B. | $\frac{12}{3x}$=$\frac{12}{x}$+$\frac{1}{2}$ | C. | $\frac{12-0.5x}{3x}$=$\frac{12}{x}$ | D. | $\frac{12-1.5x}{3x}$=$\frac{12}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com