
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
【答案】(1)证明详见解析;(2)证明详见解析;(3)10.
【解析】
试题(1)由∠DBE=∠AFE,∠BED=∠FEA,ED=EA,根据“AAS”证得△BDE≌△FAE(AAS);
(2)由全等可得AF=BD,即AF=DC,根据一组对边平行且相等的四边形的平行四边形证得四边形ADCF是平行四边形,又邻边AD=DC,所以四边形四边形ADCF是菱形;
(3)解法一:连接DF,证得四边形ABDF是平行四边形,从而得到对角线DF的长,利用菱形的对角线长求面积;
解法二:利用Rt△ABC的面积求得BC边上的高,即得到菱形ADCF中DC边上的高,利用平行四边形的面积公式求菱形的面积.
试题解析:(1)证明:在Rt△ABC中,∠BAC=![]() ,D是BC的中点,
,D是BC的中点,
∴AD=![]() BC=DC=BD,
BC=DC=BD,
∵AF∥BC,
∴∠DBE=∠AFE,
又∵E是AD中点,
∴ED=EA,
又∠BED=∠FEA,
∴△BDE≌△FAE(AAS);
(2)证明:由(1)知AF=BD,即AF=DC,
∴AF∥DC,AF=DC,
∴四边形ADCF是平行四边形,
又∵AD=DC,
∴四边形ADCF是菱形;
(3)解:(解法一)连接DF,
∵AF![]() DC,BD=CD,
DC,BD=CD,
∴AF![]() BD,
BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∴![]() ;
;
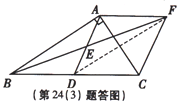
(解法二)在Rt△ABC中,AC=4,AB=5,
∴BC=![]() ,
,
设BC边上的高为![]() ,
,
则![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=16°31′,则飞机A与指挥台B的距离等于(结果保留整数)(参考数据sin16°31′=0.28,cos16°31′=0.95,tan16°31′=0.30)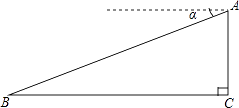
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E.F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
求证:(1)四边形AECF是平行四边形。(2)EF与GH互相平分。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
2018年10月24日港珠澳大桥正式开通,它是中国建设史上里程最长、投资最多、施工难度最大的跨海桥梁项目,体现了我国逢山开路、遇水架桥的奋斗精神,体现了我国综合国力、自主创新能力,体现了我国勇创世界一流的民族志气. 港珠澳大桥全长55公里,跨越伶仃洋,东接香港特别行政区,西接广东省珠海市和澳门特别行政区,首次实现了珠海、澳门与香港的跨海陆路连接,极大地缩短了三地间的距离. 通车前,小亮妈妈驾车从香港到珠海的陆路车程大约220公里,如果行驶的平均速度不变,港珠澳大桥通车后,小亮妈妈驾车从香港到珠海所用的行驶时间比原来缩短了2小时15分钟,求小亮妈妈原来驾车从香港到珠海需要多长时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当m≥10时为A级,5≤m<10时为B级,当0≤m<5为C级.现随机抽取30个符合年龄条件的青年人开展“每人日均发微博条数”的调查,所有抽青年人的“日均发微博条数”的数据如表:
11 | 10 | 6 | 15 | 9 | 16 | 13 | 12 | 0 | 8 | 2 | 8 | 10 | 17 | 6 |
13 | 7 | 5 | 7 | 3 | 12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
(1)求样本数据中为A级的频率;
(2)试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数;
(3)从样本数据为C级的人中随机抽取两人,用列举法求抽得两个人的“日均发微博条数”都是3的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形OABC的三个顶点A(0,10),B(8,10),C(8,0),过O、C两点的抛物线y=ax2+bx+c与线段AB交于点D,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.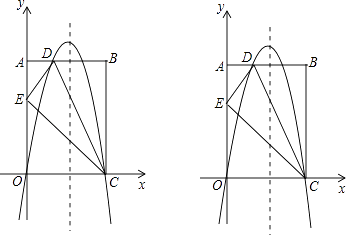
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒.请问当t为何值时,以P、Q、C为顶点的三角形是等腰三角形?
(3)若点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M、N、C、E为顶点四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以A(2,0),B(0,t)为顶点作等腰直角△ABC(其中∠ABC=90°,且点C落在第一象限内),则点C关于y轴的对称点C’的坐标为___.(用t的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,点D,E分别在AC,BC上,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若PF=2,则BP=( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com