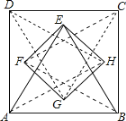
【题目】如图，分别以正方形
的四条边为边，向其内部作等边三角形，得到
、
、
、
，连接
、
、
、
，若
，则四边形
的面积为________．
【答案】
【解析】
先根据题意得出△ABE≌△BCF≌△CDG≌△DAH，连接EG并延长交CD于点M，交AB于点N，连接FH并延长交AD于点k，角BC于点l，
解：∵△ABE、△BCF、△CDG、△DAH均是以2为边长的等边三角形，
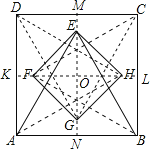
∴△ABE≌△BCF≌△CDG≌△DAH．
∵四边形ABCD是正方形，DG=CG，AE=BE，
∴点E线段AB的垂直平分线上，点G在CD的垂直平分线上，AB∥CD，
∴直线MN是线段CD与AB的垂直平分线．
∵AB=CD=2，
∴EN=
，
∴ME=2-，
同理可得GN=2-，
∴EG=2-（2--2-）=2-2．
同理可得，FH=2-2．
∵M、L、N、K分别是四边的中点，
∴EG⊥FH，且OG=OH，
∴四边形EFGH是正方形，
∴OG=OH=
EG=-1，
∴S四边形EFGH=GH2=OG2+OH2=（-1）2+（-1）2=8-4．
故答案为：8-4．
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案科目：初中数学 来源： 题型：
【题目】某学校后勤人员到文具店给八年级学生购买考试专用文具包，该文具店规定一次性购买400个以上，可享受八折优惠.若按八年级学生实际人数每人购买一个，不能享受八折优惠，需付款1936元;若再多买88个就可享受八折优惠，并且同样只需付款1936元求该校八年级学生的总人数和文具包的价格.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图矩形
的对角线
、
交于点
，过点
作
，且
，连接
，判断四边形
的形状并说明理由．
（2）如果题目中的矩形变为菱形，结论应变为什么？说明理由．
（3）如果题目中的矩形变为正方形，结论又应变为什么？说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】水龙头关闭不紧会造成滴水，小明用可以显示水量的容器做图①所示的试验，并根据试验数据绘制出图②所示的容器内盛水量W（L）与滴水时间t（h）的函数关系图象，请结合图象解答下列问题：
（1）容器内原有水多少？
（2）求W与t之间的函数关系式，并计算在这种滴水状态下一天的滴水量是多少升？
图 ① 图②
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知等边
的边长为8，点P是AB边上的一个动点(与点A、B不重合)，直线
是经过点P的一条直线，把沿直线折叠，点B的对应点是点
.
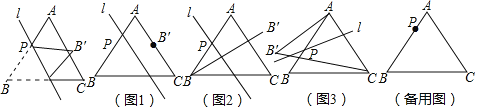
(1)如图1，当
时，若点恰好在AC边上，则
的长度为 ；
(2)如图2，当
时，若直线
，则
的长度为 ；
(3)如图3，点P在AB边上运动过程中，若直线始终垂直于AC，
的面积是否变化？若变化，说明理由；若不变化，求出面积；
(4)当
时，在直线变化过程中，求面积的最大值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请阅读下列材料：
问题：如图，在正方形
和平行四边形
中，点
，
，
在同一条直线上，
是线段
的中点，连接
，
．
探究：当与的夹角为多少度时，平行四边形是正方形？
小聪同学的思路是：首先可以说明四边形是矩形；然后延长
交
于点
，构造全等三角形，经过推理可以探索出问题的答案．
请你参考小聪同学的思路，探究并解决这个问题．
（1）求证：四边形是矩形；
（2）与的夹角为________度时，四边形是正方形．
理由：
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，∠QPN的顶点P在正方形ABCD两条对角线的交点处，∠QPN=α，∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F（点F与点C、D不重合）．
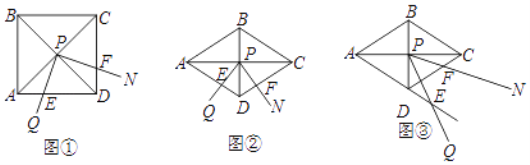
(1)如图①，当α=90°时，求证：DE+DF=AD．
(2)如图②，将图①中的正方形ABCD改为∠ADC=120°的菱形，其他条件不变，当α=60°时，(1)中的结论变为
，请给出证明．
(3)在(2)的条件下，将∠QPN绕点P旋转，若旋转过程中∠QPN的边PQ与边AD的延长线交于点E，其他条件不变，探究在整个运动变化过程中，DE，DF，AD之间满足的数量关系，直接写出结论，不用加以证明．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
