(2007•淄川区二模)课间休息时,同学们到饮水机旁依次每人接水0.25升,他们先打开了一个饮水管,后来又打开了第二个饮水管.假设接水的过程中每根饮水管出水的速度是匀速的,在不关闭饮水管的情况下,饮水机水桶内的存水量y(升)与接水时间x(分)的函数关系图象如图所示.请结合图象回答下列问题:
(1)存水量y(升)与接水时间x(分)的函数关系式;
(2)如果接水的同学有28名,那么他们都接完水需要几分钟?
(3)如果有若干名同学按上述方法接水,他们接水所用时间要比只开第一个饮水管接水的时间少用2分钟,那么有多少名学生接完水?



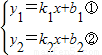 ,
,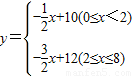 ;
; x+12,
x+12,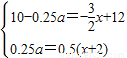 ,
,
