
| 套 | A种塑料(吨) | B种塑料(吨) | |
| M型滑梯 | 80-x | 0.6(80-x) | 0.9(80-x) |
| N型滑梯 | x | 1.1x | 0.4x |
| 合计 | 80 | 70 | 52 |
分析 (1)根据题意和表格中的数据可以把表格中未填写的补充完整;
(2)根据题意可知需要的A种塑料不多于70吨,B种塑料不多于52吨,从而可以列出不等式组,求出x的取值范围;
(3)根据表格中的数据和题意可以写出y与x的函数关系式;
(4)根据题意可以写出利润与x的函数关系,再根据x的取值范围,从而可以求得最大利润.
解答 解:(1)由题意可得,
当生产N型滑梯x套时,生产M型滑梯为(80-x)套,则需要A种塑料0.6(80-x),B种塑料0.9(80-x),
当生产N型滑梯x套时,则需要A种塑料1.1x,B种塑料0.4x,
故答案为:80-x、0.6(80-x)、0.9(80-x),1.1x、0.4x;
(2)由题意可得,
$\left\{\begin{array}{l}{0.6(80-x)+1.1x≤70}\\{0.9(80-x)+0.4x≤52}\end{array}\right.$,
解得,40≤x≤44,
答:N型滑梯的数量应控制在40≤x≤44范围内;
(3)由题意可得,
y=4500(80-x)+5000x=500x+360000,
即y与x的函数关系式为y=500x+360000;
(4)∵y=500x+360000,40≤x≤44,
∴当x=44时,y取得最大值,此时y=500×44+360000=22000+360000=382000,
答:生产N型滑梯44套时所获利润最大,最大利润是382000元.
点评 本题考查一次函数的应用,解答此类题目的关键是明确题意,找出所求问题需要的条件,利用函数的思想和不等式的性质解答.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
| 家用电器 | 进价(元/件) | 售价(元/件) |
| A | m+200 | 1800 |
| B | m | 1700 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
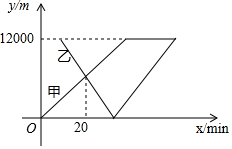 甲旅游船上午9:00从嘉荫码头出发逆水而上匀速开往花骨山景区,10min后乙旅游船从龙骨山景区匀速返回嘉荫码头接送游客,游客上船后又立即起航开往龙骨山(游客上下船时间忽略不计),到达龙骨山时恰好10:00,此时甲船已到达20min,若甲船从码头出发后所用时间为x(单位:min),则甲、乙两船与嘉荫码头的距离y(单位:m)关于x的函数关系图象如图所示,请结合图象信息,解答下列问题:
甲旅游船上午9:00从嘉荫码头出发逆水而上匀速开往花骨山景区,10min后乙旅游船从龙骨山景区匀速返回嘉荫码头接送游客,游客上船后又立即起航开往龙骨山(游客上下船时间忽略不计),到达龙骨山时恰好10:00,此时甲船已到达20min,若甲船从码头出发后所用时间为x(单位:min),则甲、乙两船与嘉荫码头的距离y(单位:m)关于x的函数关系图象如图所示,请结合图象信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
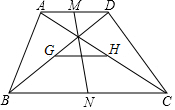 如图,在四边形ABCD中,BD和AC是它的两条对角线,点M、N分别为AD、BC的中点,点G、H分别为BD、AC的中点,求证:MN与GH互相平分.
如图,在四边形ABCD中,BD和AC是它的两条对角线,点M、N分别为AD、BC的中点,点G、H分别为BD、AC的中点,求证:MN与GH互相平分.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
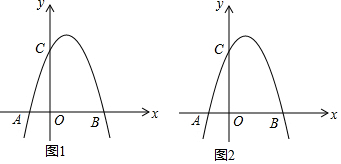 如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax-3a与x轴交于A、B两点,与y轴交于点C,BO=CO.
如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax-3a与x轴交于A、B两点,与y轴交于点C,BO=CO.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com