
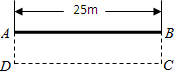
 ,为了节约材料同时要使矩形的面积最大,他利用了自家房屋一面长25m的墙,设计了如图一个矩形ABCD的羊圈.
,为了节约材料同时要使矩形的面积最大,他利用了自家房屋一面长25m的墙,设计了如图一个矩形ABCD的羊圈. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
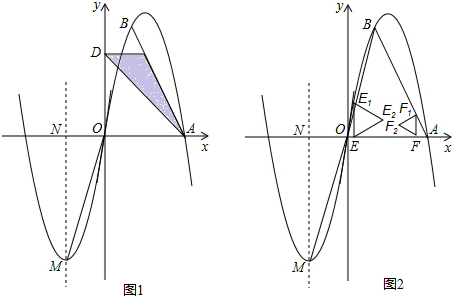
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
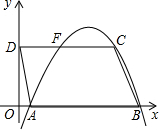 于F,线段AD所在直线的函数解析式为y=-3x+3.
于F,线段AD所在直线的函数解析式为y=-3x+3.| 1 |
| 6 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
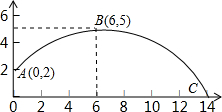 某个二次函数图象的一部分,如图所示,如果这个男同学的出手处A点的坐标(0,2),铅球路线的最高处B点的坐标为(6,5).
某个二次函数图象的一部分,如图所示,如果这个男同学的出手处A点的坐标(0,2),铅球路线的最高处B点的坐标为(6,5).| 15 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | -6 | -8 | -6 | 0 | … |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
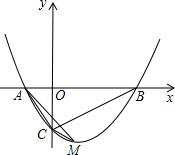 交l于点P,M为此抛物线的顶点.若四边形PEMF是有一个内角为60°的菱形,求此抛物线的解析式.
交l于点P,M为此抛物线的顶点.若四边形PEMF是有一个内角为60°的菱形,求此抛物线的解析式.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
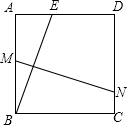 M,交DC于N.
M,交DC于N.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
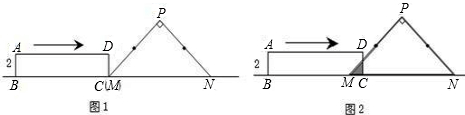
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com