
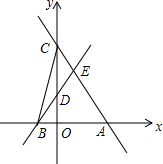
 直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点C,过点B(-1,0)的直线交线段OC于点D,交线段AC于点E,连接BC,△CDB的面积为1.
直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点C,过点B(-1,0)的直线交线段OC于点D,交线段AC于点E,连接BC,△CDB的面积为1.分析 (1)对于已知直线解析式,分别令x与y为0求出y与x的值,确定出A与C坐标,得出OA与OC的长,由B的坐标确定出OB的长,三角形CBD面积等于底边CD与高OB乘积的一半,求出CD的长,由OC-CD求出OD的长,确定出D坐标,设直线BE解析式为y=kx+b,把B与D坐标代入求出k与b的值,确定出直线BE解析式,与已知直线联立求出E的坐标即可;
(2)四边形AODE面积等于三角形AOC面积减去三角形CDE面积,求出即可;
(3)如图所示,若四边形DPQE为矩形,则有DP与DE垂直,根据直线DE,求出直线DP解析式,与已知直线联立求出P坐标即可.
解答 解:(1)对于直线y=-$\frac{4}{3}$x+4,
令x=0,得到y=4;令y=0,得到x=3,
∴C(0,4),A(3,0),即OC=4,OA=3,
∵BO=1,△CBD面积为1,
∴$\frac{1}{2}$CD•BO=1,即CD=2,
∴OD=OC-CD=4-2=2,即D(0,2),
设直线BD解析式为y=kx+b,
把B与D坐标代入得:$\left\{\begin{array}{l}{b=2}\\{-k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=2}\end{array}\right.$,即直线BD解析式为y=2x+2,
联立得:$\left\{\begin{array}{l}{y=2x+2}\\{y=-\frac{4}{3}x+4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=0.6}\\{y=3.2}\end{array}\right.$,即E(0.6,3.2);
(2)S四边形AODE=S△COA-S△CDE=$\frac{1}{2}$×3×4-$\frac{1}{2}$×2×0.6=6-0.6=5.4;
(3)如图所示:
当四边形DPQE为矩形时,DP⊥DE,
∵直线DE解析式为y=2x+2,D坐标为(0,2),
∴直线DP解析式为y-2=-$\frac{1}{2}$x,即y=-$\frac{1}{2}$x+2,
联立得:$\left\{\begin{array}{l}{y=-\frac{1}{2}x+2}\\{y=-\frac{4}{3}x+4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2.4}\\{y=0.8}\end{array}\right.$,
则P(2.4,0.8).
点评 此题属于一次函数综合题,涉及的知识有:待定系数法求一次函数解析式,一次函数与坐标轴的交点,坐标与图形性质,两直线交点坐标的求法,两直线垂直时斜率的乘积为-1,以及矩形的性质,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,是某公司一电热淋浴器水箱的水量y(升)与供水时间x(分)的函数关系.
如图所示,是某公司一电热淋浴器水箱的水量y(升)与供水时间x(分)的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
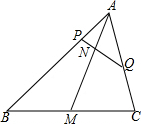 如图,已知△ABC,AM是中线,点P在边AB上,点Q在边AC上,PQ交AM于点N.
如图,已知△ABC,AM是中线,点P在边AB上,点Q在边AC上,PQ交AM于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在四边形ABCD中,AB=CD,AD=BC,试判断AB与CD、AD与BC之间有什么样的位置关系,说明理由.除前面的结论外.你还能得到哪些结论?请写出来.
在四边形ABCD中,AB=CD,AD=BC,试判断AB与CD、AD与BC之间有什么样的位置关系,说明理由.除前面的结论外.你还能得到哪些结论?请写出来.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2(y+z)}{x+3(y+z)}$=$\frac{2}{x+3}$ | B. | $\frac{x+y}{{x}^{2}+{y}^{2}}$=$\frac{2}{x+y}$ | ||
| C. | $\frac{(x-y)^{2}}{(y-x)^{2}}$=-1 | D. | $\frac{y-x}{2xy-{x}^{2}-{y}^{2}}$=$\frac{1}{x-y}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com