
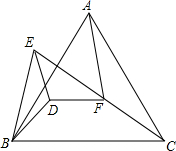
 如图所示,△ABC为等边三角形,DB=DE,∠BDE=120°,F为CE的中点,求证:AF⊥DF.
如图所示,△ABC为等边三角形,DB=DE,∠BDE=120°,F为CE的中点,求证:AF⊥DF. 分析 作AM⊥BC于M,作DN⊥BE于N.延长ND交FM于H,连结FN,如图,根据等边三角形的性质得BM=CM,AM=$\sqrt{3}$BM,再根据等腰三角形的性质和含30度的直角三角形三边的关系得到BN=EN,EN=$\sqrt{3}$DN,则可判断FN、FM为△EBC的中位线,所以FN=$\frac{1}{2}$BC=BM,FN∥BC,FM=$\frac{1}{2}$BE=EN,则AM⊥NF,NH⊥FM,于是可利用等角的余角相等可得∠DNF=∠HMA,加上$\frac{FM}{DN}$=$\frac{AM}{NF}$=$\sqrt{3}$,则可判断△AMF∽△FND得到∠FAM=∠NFD,接着计算出∠AFD=90°,所以AF⊥DF.
解答 证明:作AM⊥BC于M,作DN⊥BE于N.延长ND交FM于H,连结FN,如图,
∵△ABC为等边三角形,
∴BM=CM,AM=$\sqrt{3}$BM,
∵DB=DE,∠BDE=120°,
∴BN=EN,∠DEN=30°,
∴EN=$\sqrt{3}$DN,
∵F为CE的中点,
∴FN、FM为△EBC的中位线,
∴FN=$\frac{1}{2}$BC=BM,FN∥BC,FM=$\frac{1}{2}$BE=EN,
∴AM⊥NF,NH⊥FM,
∴∠DNF=∠HMA,
∵$\frac{FM}{DN}$=$\frac{EN}{DN}$=$\sqrt{3}$,$\frac{AM}{NF}$=$\frac{AM}{BM}$=$\sqrt{3}$,
∴$\frac{FM}{DN}$=$\frac{AM}{NF}$,
∴△AMF∽△FND,
∴∠FAM=∠NFD,
∴∠AFN+∠NFD=∠FAM+∠AFN=90°,即∠AFD=90°,
∴AF⊥DF.
点评 本题考查了三角形相似的判定与性质:寻找相似三角形的一般方法是通过作平行线构造相似三角形;或依据基本图形对图形进行分解、组合;利用三角形相似的性质计算有关线段的长.也考查了三角形中位线定理和等边三角形的性质.


科目:初中数学 来源: 题型:解答题
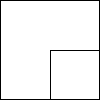 如图是一幅“斜阳正方形”,最大正方形的边长为a米,第二个正方形的边长是$\frac{a}{2}$米,第三个正方形的边长是$\frac{a}{4}$米,…以此类推.
如图是一幅“斜阳正方形”,最大正方形的边长为a米,第二个正方形的边长是$\frac{a}{2}$米,第三个正方形的边长是$\frac{a}{4}$米,…以此类推.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 纳税级数 | 个人每月应纳税所得额 | 税率 |
| 1 | 不超过1500元的部分 | 3% |
| 2 | 超过1500元至4500元的部分 | 10% |
| 3 | 超过4500元至9000元的部分 | 20% |
| 4 | 超过9000元至35000元的部分 | 25% |
| 5 | 超过35000元至55000元的部分 | 30% |
| 6 | 超过55000元至80000元的部分 | 35% |
| 7 | 超过80000元的部分 | 45% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果∠AOB=∠COD,那么$\widehat{AB}$=$\widehat{CD}$ | B. | 如果$\widehat{AB}$=$\widehat{CD}$,那么∠AOB=∠COD | ||
| C. | 如果$\widehat{AB}$=$\widehat{CD}$,那么AB=CD | D. | 如果AB=CD,那么$\widehat{AB}$=$\widehat{CD}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
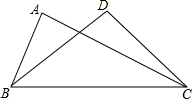 如图,在△ABC和△DCB中,AB=DC,下列四个条件:①AC=DB;②∠A=∠B; ③∠ABC=∠DCB;④∠ACB=∠DBC中,添加其中的一个条件不能使△ABC≌△DCB的有( )
如图,在△ABC和△DCB中,AB=DC,下列四个条件:①AC=DB;②∠A=∠B; ③∠ABC=∠DCB;④∠ACB=∠DBC中,添加其中的一个条件不能使△ABC≌△DCB的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com