
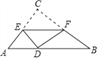
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4.翻折∠C,使点C落在斜边上某一点D处,折痕为EF(点E、F分别在边AC、BC上).若△CEF与△ABC相似,则AD的长为_____.
【答案】![]() 或
或![]()
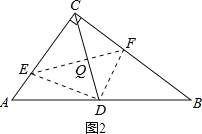
【解析】分析:若△CEF与△ABC相似,分两种情况:①若若CE:CF=3:4,如图1所示,此时EF∥AB. CD为AB边上的高,②若CF:CE=3:4,如图2所示.由相似三角形角之间的关系,可以推出∠A=∠ECD,与∠CEF=∠B.从而得到![]() ,即D点为AB的中点.
,即D点为AB的中点.
详解:若△CEF与△ABC相似,分两种情况:
若CE:CF=3:4,如图1所示:

∵CE:CF=AC:BC,
∴EF∥AB.
由折叠性质可知,CD⊥EF,
∴CD⊥AB,即此时CD为AB边上的高,
在Rt△ABC中,∵![]()
∴![]()
∴![]()
∴AD=ACcosA=![]()
若CF:CE=3:4,如图2所示:
∵△CEF∽△CBA,
∴∠CEF=∠B.
由折叠性质可知,![]()
又∵![]()
∴∠A=∠ECD,
∴AD=CD.
同理可得:∠B=∠FCD,CD=BD,
∴D点为AB的中点,
∴![]()
综上所述,AD的长为![]() 或
或![]()
故答案为:![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
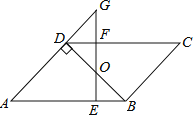
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年1月的日历表如表所示:
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | |||
5 | 6 | 7 | 8 | 9 | 10 | 11 |
12 | 13 | 14 | 15 | 16 | 17 | 18 |
19 | 20 | 21 | 22 | 23 | 24 | 25 |
26 | 27 | 28 | 29 | 30 | 31 |
快到放寒假了,班主任孙老师看日历届时准备安排一节假期安全班会课,孙老师把日历与本学期书本上73页的数学活动3联系在一起,经过思索后,孙老师给孩子们展示两个问题:
(1)若连续三天的号数之和等于48,那么这三天分别是几号?
(2)用一个“T”字形的框在表中框出四个数,这四个数的和能等于83吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列各题并按要求完成:
(1)定义:若两个一元二次方程有一个相同的实数根,则称这两个方程为“友好方程”,已知关于x的一元二次方程 x 2x 0 与 x 3x m 1 0 为“友好方程”,求 m 的值;
(2)关于x的一元二次方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,
,![]() ,且二次根式
,且二次根式![]() 有意义,若T=
有意义,若T=![]() ,求T的取值范围;
,求T的取值范围;
(3)我们不妨约定方程的整数解称之为“硬核”,例如x=1就称为方程(x-1)(2x+1)=0 的一个“硬核”,若一元二次方程(k-3k+2)x+(2k-4k+1)x+k-k=0(k为常数)有两个不同的“硬核”,试确定方程的两个“硬核”及常数 k 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),一架长4米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子与地面的倾斜角α为60°.
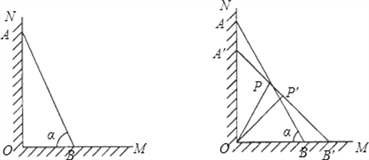
(1)求AO与BO的长;
(2)若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行.如图(2),当A点下滑到A′点,B点向右滑行到B′点时,梯子AB的中点P也随之运动到P′点,若∠POP′=15°,试求AA′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:我国数学家华罗庚在一次出国访问途中,看到飞机上:邻座的乘客阅读的杂志上有一道智力题,求59319的立方根,华罗庚脱口而击.众人惊命,忙问计算奥妙.你知道怎样迅速准确地计算出结果的吗?诺按照下面的分析试一试
(1)由103=1000,1003=100000,可知![]() 是 位数;
是 位数;
(2)由59319的个位数是9,可知![]() 的个位数是 ;
的个位数是 ;
(3)如果划去59319后面的三位319得到59,而33=27,43=64,由此确定![]() 的十位数是 .
的十位数是 .
请应用以上方法计算:![]() = .
= . ![]() =
=
查看答案和解析>>
科目:初中数学 来源: 题型:
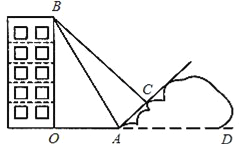
【题目】某校九年级的小红同学,在自己家附近进行测量一座楼房高度的实践活动.如图,她在山坡坡脚A出测得这座楼房的楼顶B点的仰角为60°,沿山坡往上走到C处再测得B点的仰角为45°.已知OA=200m,此山坡的坡比i=![]() ,且O、A、D在同一条直线上.
,且O、A、D在同一条直线上.
求:(1)楼房OB的高度;
(2)小红在山坡上走过的距离AC.(计算过程和结果均不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初中各年级学生每天的平均睡眠时间(单位:h,精确到1 h),抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
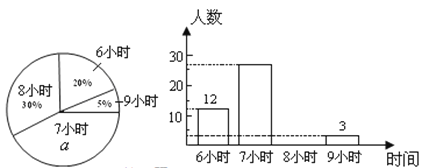
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数![]() 的值为_______,所抽查的学生人数为______;
的值为_______,所抽查的学生人数为______;
(2)求出平均睡眠时间为8小时的人数,并补全条形图;
(3)求出这部分学生的平均睡眠时间的平均数;
(4)如果该校共有学生1200名,请你估计睡眠不足(少于8小时)的学生数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com