
【题目】观察下表中的数据信息:

根据表中的信息判断,下列语句中正确的是( )
A.![]() 1.53
1.53
B.241的算术平方根比15.5小
C.根据表中数据的变化趋势,可以推断出16.12将比256增大3.17
D.只有3个正整数n满足15.7![]() 15.8
15.8
 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】有以下运算程序,如图所示:
![]()
比如,输入数对(2,1),输出W=2.
(1)若输入数对(1,﹣2),则输出W= ;
(2)分别输入数对(m,﹣n)和(﹣n,m),输出的结果分别是W1,W2,试比较W1,W2的大小,并说明理由;
(3)设a=|x﹣2|,b=|x﹣3|,若输入数对(a,b)之后,输出W=26,求a+b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一列有理数﹣1,2,﹣3,4,﹣5,6,…如图所示有序排列,根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰6”中C的位置是有理数_____,﹣2019应排在A、B、C、D、E中的_____位置.
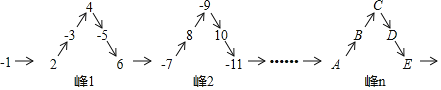
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,我市城区四校决定联合购买一批足球运动装备.市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打七折.
(1)求每套队服和每个足球的价格分别是多少元?
(2)若城区四校联合购买100套队服和a(a>10)个足球,请用含a的代数式分别表示出到甲商场和乙商场购买装备所花费用;
(3)在(2)的条件下,当a=65时,你认为到甲、乙哪家商场购买比较合算?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种盛酒的桶,已知10个大桶加上2个小桶可以盛酒6斛(斛,音hu,是古代的一种容量单位),3个大桶加上15个小桶也可以盛酒6斛.
(1)求1个大桶可盛酒多少斛?
(2)分析2个大桶加上3个小桶可以盛酒2斛吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请仔细阅读下面两则材料,然后解决问题:
材料1:小学时我们学过,任何一个假分数都可以化为一个整数与一个真分数的和的形式,同样道理,任何一个分子次数不低于分母次数的分式都可以化为一个整式与另一个分式的和(或差)的形式,其中分式的分子次数低于分母次数.
如:![]() .
.
材料2:对于式子![]() ,利用换元法,令
,利用换元法,令![]() ,
,![]() .则由于
.则由于![]() ,所以反比例函数
,所以反比例函数![]() 有最大值,且为3.因此分式
有最大值,且为3.因此分式![]() 的最大值为5.
的最大值为5.
根据上述材料,解决下列问题:
(1)把分式![]() 化为一个整式与另一个分式的和的形式,其中分式的分子次数低于分母次数.
化为一个整式与另一个分式的和的形式,其中分式的分子次数低于分母次数.
(2)当![]() 的值变化时,求分式
的值变化时,求分式![]() 的最大(或最小)值.
的最大(或最小)值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个能被13整除的自然数我们称为“十三数”,“十三数”的特征是:若把这个自然数的末三位与末三位以前的数字组成的数之差,如果能被13整除,那么这个自然数就一定能被13整除.例如:判断383357能不能被13整除,这个数的末三位数字是357,末三位以前的数字组成的数是383,这两个数的差是383﹣357=26,26能被13整除,因此383357是“十三数”.
(1)判断3253和254514是否为“十三数”,请说明理由.
(2)若一个四位自然数,千位数字和十位数字相同,百位数字与个位数字相同,则称这个四位数为“间同数”.
①求证:任意一个四位“间同数”能被101整除.
②若一个四位自然数既是“十三数”,又是“间同数”,求满足条件的所有四位数的最大值与最小值之差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )
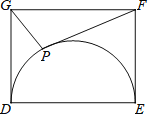
A. ![]() B.
B. ![]() C. 34 D. 10
C. 34 D. 10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com