
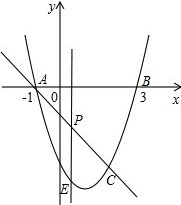
 ��ͼ��������y=x2-2x-3��x�ύA��B���㣨A����B����ࣩ��ֱ��l�������߽���A��C���㣬����C��ĺ�����Ϊ2��
��ͼ��������y=x2-2x-3��x�ύA��B���㣨A����B����ࣩ��ֱ��l�������߽���A��C���㣬����C��ĺ�����Ϊ2������ ��1����y=0�õ�����x�ķ��̣��ⷽ�̿���õ�A�͵�B�ĺ����꣬��x=2���������ߵĽ���ʽ��ö�Ӧ��yֵ����õ�C�������꣬��ֱ��AC�Ľ���ʽΪy=kx+b������A�͵�C������������k��b��ֵ���ɣ�
��2����P��ĺ�����Ϊx��-1��x��2����P��E������ֱ�Ϊ��P��x��-x-1����E��x��x2-2x-3����Ȼ��õ�PE��x�ĺ�����ϵʽ�����ö��κ��������ʿ����PE�����ֵ���������S��ACE=$\frac{1}{2}$��PE����xC-xA����⼴�ɣ�
��3�����F������Ϊ��a��0������G������Ϊ��x��y���������е����깫ʽ��õ�G�����꣬Ȼ��G��������������ߵĽ���ʽ��ö�Ӧ��a��ֵ���ɣ�
��� �⣨1����y=0ʱ�����x1=-1��x2=3��
��A��-1��0��B��3��0����
��C������x=2����y=x2-2x-3��y=-3��
��C��2��-3����
��ֱ��AC�Ľ���ʽΪy=kx+b������A�͵�C���������ã�$\left\{\begin{array}{l}{-k+b=0}\\{2k+b=-3}\end{array}\right.$��
��ã�k=-1��b=-1��
��ֱ��AC�ĺ�������ʽ��y=-x-1��
��2����P��ĺ�����Ϊx��-1��x��2����P��E������ֱ�Ϊ��P��x��-x-1����E��x��x2-2x-3��
��P����E����Ϸ���
��PE=��-x-1��-��x2-2x-3��=-x2+x+2=-��x-$\frac{1}{2}$��2+$\frac{9}{4}$��
�൱x=$\frac{1}{2}$ʱ��PE�����ֵΪ$\frac{9}{4}$��
��S��ACE=$\frac{1}{2}$��PE����xC-xA��=$\frac{1}{2}$��$\frac{9}{4}$��3=$\frac{27}{8}$��
��3����ACΪƽ���ı��εĶԽ���ʱ�����F������Ϊ��a��0������G������Ϊ��x��y����
��ƽ���ı��εĶԽ�����ƽ�֣�
�������е����깫ʽ��֪��$\frac{0+y}{2}=\frac{-3+0}{2}$��$\frac{a+x}{2}=\frac{-1+2}{2}$��
��y=-3��x=1-a��
�ߵ�G���������ϣ�
��-3=��1-a��2-2��1-a��-3�������ã�a2-1=0�����a=-1��a=-1����ȥ����
���F��������1��0����
��ACΪƽ���ı��εıߣ�CFΪ�Խ���ʱ�����F������Ϊ��a��0������G������Ϊ��x��y����
��ƽ���ı��εĶԽ�����ƽ�֣�
�������е����깫ʽ��֪��$\frac{a+2}{2}=\frac{-1+x}{2}$��$\frac{-3+0}{2}$=$\frac{0+y}{2}$��
��y=-3��x=a+3
�ߵ�G���������ϣ�
��-3=��a+3��2-2��a+3��-3�������ã�a2+4a+3=0����a=-3��a=-1����ȥ��
���F��������-3��0����
��ACΪƽ���ı��εıߣ�CGΪ�Խ���ʱ�����F������Ϊ��a��0������G������Ϊ��x��y����
��ƽ���ı��εĶԽ�����ƽ�֣�
�������е����깫ʽ��֪��$\frac{-1+a}{2}=\frac{2+x}{2}$��$\frac{0+0}{2}$=$\frac{-3+y}{2}$��
��y=3��x=a-3
�ߵ�G���������ϣ�
��3=��a-3��2-2��a-3��-3�������ã�a2-8a+9=0�����a=4+$\sqrt{7}$��a=4$-\sqrt{7}$��
���F��������4+$\sqrt{7}$��0����4-$\sqrt{7}$����
������������F��������1��0����-3��0����4+$\sqrt{7}$��0����4-$\sqrt{7}$����
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ������һ�κ����Ľ���ʽ�����κ��������ʡ�ƽ���ı��ε����ʣ��е����깫ʽ���г�PE��x�ĺ�����ϵʽ�ǽ�����⣨2���Ĺؼ��������е����깫ʽ�õ���G�������ǽ�����⣨3���Ĺؼ���


 ��ʦ����ָ���ο�ʱϵ�д�
��ʦ����ָ���ο�ʱϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��AB��CD��AE��CD�ڵ�C��DE��AE�ڵ�E������A=42�㣬���D=��������
��ͼ��AB��CD��AE��CD�ڵ�C��DE��AE�ڵ�E������A=42�㣬���D=��������| A�� | 42�� | B�� | 58�� | C�� | 52�� | D�� | 48�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com