
【题目】如图,线段AB=8,射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且点C、D与点B在AP两侧,在线段DP上取一点E,使∠EAP=∠BAP,直线CE与线段AB相交于点F(点F与点A、B不重合).
(1)求证:△AEP≌△CEP;
(2)判断CF与AB的位置关系,并说明理由;
(3)求△AEF的周长.
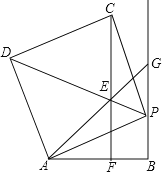
【答案】(1)见解析;(2)CF⊥AB,见解析;(3)16
【解析】
(1)四边形APCD正方形,则DP平分∠APC,PC=PA,∠APD=∠CPD=45°,即可求解;
(2)△AEP≌△CEP,则∠EAP=∠ECP,而∠EAP=∠BAP,则∠BAP=∠FCP,又∠FCP+∠CMP=90°,则∠AMF+∠PAB=90°即可求解;
(3)证明△PCN≌△APB(AAS),则CN=PB=BF,PN=AB,即可求解.
(1)证明:∵四边形APCD正方形,
∴DP平分∠APC,PC=PA,
∴∠APD=∠CPD=45°,
∴△AEP≌△CEP(SAS);
(2)CF⊥AB,理由如下:
∵△AEP≌△CEP,
∴∠EAP=∠ECP,
∵∠EAP=∠BAP,
∴∠BAP=∠FCP,
∵∠FCP+∠CMP=90°,∠AMF=∠CMP,
∴∠AMF+∠PAB=90°,
∴∠AFM=90°,
∴CF⊥AB;
(3)过点 C 作CN⊥PB.
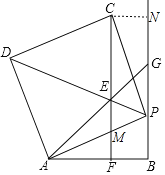
∵CF⊥AB,BG⊥AB,
∴FC∥BN,
∴∠CPN=∠PCF=∠EAP=∠PAB,
又AP=CP,
∴△PCN≌△APB(AAS),
∴CN=PB=BF,PN=AB,
∵△AEP≌△CEP,
∴AE=CE,
∴AE+EF+AF
=CE+EF+AF
=BN+AF
=PN+PB+AF
=AB+CN+AF
=AB+BF+AF
=2AB
=16.


科目:初中数学 来源: 题型:
【题目】阅读以下材料:对数的创始人是苏格兰数学家纳皮尔,纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉才发现指数与对数之间的联系.
对数的定义:一般地,若ax=N(a>0,a≠1),那么x叫做以a为底N的对数,记作:记作:x=logaN.比如指数式24=16可以转化为4=log216,对数式2=log525可以转化为52=25.
我们根据对数的定义可得到对数的一个性质:
loga(MN)=logaM+logaN(a>0,a≠1,M>0,N>0);理由如下:logaM=m,logaN=n,则M=am,N=an
∴MN=aman=am+n,由对数的定义得m+n=loga(MN)
又∵m+n=logaM+logaN
∴loga(MN)=logaM+logaN
解决以下问题:
(1)将指数式53=125转化为对数式 ;
(2)log24= ,log381= ,log464= .(直接写出结果)
(3)证明:证明loga![]() =logaM﹣logaN(a>0,a≠1,M>0,N>0).(写出证明过程)
=logaM﹣logaN(a>0,a≠1,M>0,N>0).(写出证明过程)
(4)拓展运用:计算计算log34+log312﹣log316= .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
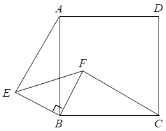
【题目】如图,△EBF为等腰直角三角形,点B为直角顶点, 四边形ABCD是正方形.
⑴ 求证:△ABE≌△CBF;
⑵ CF与AE有什么特殊的位置关系?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】思维探索:
在正方形ABCD中,AB=4,∠EAF的两边分别交射线CB,DC于点E,F,∠EAF=45°.
(1)如图1,当点E,F分别在线段BC,CD上时,△CEF的周长是 ;
(2)如图2,当点E,F分别在CB,DC的延长线上,CF=2时,求△CEF的周长;
拓展提升:
如图3,在Rt△ABC中,∠ACB=90°,CA=CB,过点B作BD⊥BC,连接AD,在BC的延长线上取一点E,使∠EDA=30°,连接AE,当BD=2,∠EAD=45°时,请直接写出线段CE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,E是矩形ABCD的边BC上一点,EF⊥AE,分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.
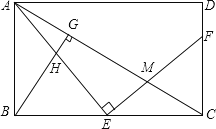
(1)求证:△ABE∽△ECF;
(2)找出与△ABH相似的三角形,并证明;
(3)若E是BC中点,BC=2AB,AB=4,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴快车是一种便捷的出行工具,某地的计价规则如下表:
计费项目 | 里程费 | 时长费 | 远途费 |
单价 | 2元/公里 |
| 1元/公里 |
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收1元. | |||
小李与小张分别从不同地点,各自同时乘坐滴滴快车,到同一地点相见,已知到达约定地点时他们的实际行车里程分别为7公里与9公里,两人付给滴滴快车的乘车费相同.其中一人先到达约定地点,他等候另一人的时间等于他自己实际乘车时间,且恰好是另一人实际乘车时间的一半,则小李的乘车费为______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E是边BC上一点,连接AE,过点E作EM⊥AE,交对角线AC于点M,过点M作MN⊥AB,垂足为N,连接NE.


(1)求证:AE=![]() NE+ME;
NE+ME;
(2)如图2,延长EM至点F,使EF=EA,连接AF,过点F作FH⊥DC,垂足为H.猜想CH与FH存在的数量关系,并证明你的结论;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代第一部数学专著,它的出现标志中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》中:“今有竹高一丈,末折抵地,去本四尺,问折者高几何?”意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远(如图),则折断后的竹子高度为多少尺?(1丈=10尺)( )
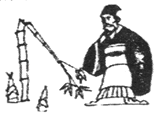
A.3B.5C.4.2D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民区内的“广场舞”引起媒体关注,民勤电视台为此进行过专访报到.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:![]() .非常赞同;
.非常赞同;![]() .赞同但要有时间限制;
.赞同但要有时间限制;![]() .无所谓;
.无所谓;![]() .不赞同.并将调查结果绘制了图①和图②两幅不完整的统计图.请你根据图中提供的信息解答下列问题:
.不赞同.并将调查结果绘制了图①和图②两幅不完整的统计图.请你根据图中提供的信息解答下列问题:

(1)求本次被抽查的居民有多少人?
(2)将图①和图②补充完整.
(3)求图②中“![]() ”层次所在扇形的圆心角度数.
”层次所在扇形的圆心角度数.
(4)估计该小区5000名居民中对“广场舞”的看法表示赞同(包括![]() 层次和
层次和![]() 层次)的大约有多少人.
层次)的大约有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com