
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.
如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.
(1) 请你求出“蛋圆”抛物线部分的解析式,并写出自变量的取值范围;
(2)你能求出经过点C的“蛋圆”切线的解析式吗?试试看;
(3)开动脑筋想一想,相信你能求出经过点D的“蛋圆”切线的解析式.
解:(1)解法1:根据题意可得:A(-1,0),B(3,0);
则设抛物线的解析式为![]() (a≠0)
(a≠0)
又点D(0,-3)在抛物线上,∴a(0+1)(0-3)=-3,解之得:a=1
∴y=x2-2x-3
自变量范围:-1≤x≤3
解法2:设抛物线的解析式为![]() (a≠0)
(a≠0)
根据题意可知,A(-1,0),B(3,0),D(0,-3)三点都在抛物线上
∴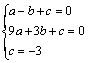 ,解之得:
,解之得:![]()
∴y=x2-2x-3
自变量范围:-1≤x≤3
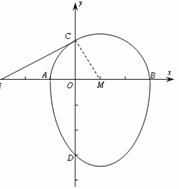
(2)设经过点C“蛋圆”的切线CE交x轴于点E,连结CM,
在Rt△MOC中,∵OM=1,CM=2,∴∠CMO=60°,OC=![]()
在Rt△MCE中,∵OC=2,∠CMO=60°,∴ME=4
∴点C、E的坐标分别为(0,![]() ),(-3,0)
),(-3,0)
∴切线CE的解析式为![]()
(3)设过点D(0,-3),“蛋圆”切线的解析式为:y=kx-3(k≠0)
由题意可知方程组![]() 只有一组解
只有一组解
即![]() 有两个相等实根,∴k=-2
有两个相等实根,∴k=-2
∴过点D“蛋圆”切线的解析式y=-2x-3。


科目:初中数学 来源: 题型:
 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,点D的坐标为(0,-3)AB为半圆直径,半圆圆心M(1,0),半径为2,则“蛋圆”的抛物线部分的解析式为
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,点D的坐标为(0,-3)AB为半圆直径,半圆圆心M(1,0),半径为2,则“蛋圆”的抛物线部分的解析式为查看答案和解析>>
科目:初中数学 来源: 题型:
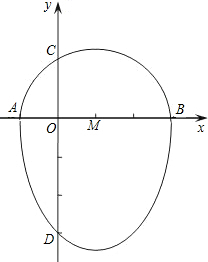 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图所示,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图所示,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.查看答案和解析>>
科目:初中数学 来源: 题型:
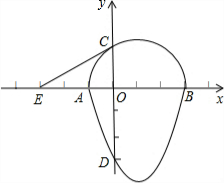 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2,则经过点C的“蛋圆”切线EC的解析式是
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A,B,C,D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2,则经过点C的“蛋圆”切线EC的解析式是查看答案和解析>>
科目:初中数学 来源: 题型:
 正确?提出你的见解,若△BDE的面积存在最大值,请求出m的值以及点E的坐标.
正确?提出你的见解,若△BDE的面积存在最大值,请求出m的值以及点E的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 仔细阅读并完成下题:
仔细阅读并完成下题:| 3 |
| 3 |
| 7 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com