
【题目】△ABC在平面直角坐标系中如图:
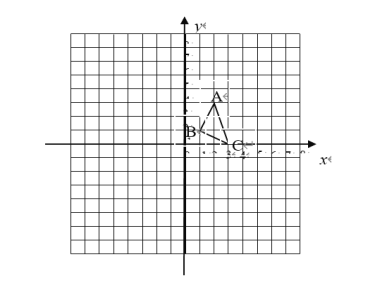
(1)画出将△ABC绕点O逆时针旋转90°所得到的![]() ,并写出
,并写出![]() 点的坐标.
点的坐标.
(2)画出将△ABC关于x轴对称的![]() ,并写出
,并写出![]() 点的坐标.
点的坐标.
(3)求在旋转过程中线段OA扫过的图形的面积.
【答案】(1)![]() (-3,2);(2)
(-3,2);(2)![]() (2,-3);(3)S=
(2,-3);(3)S=![]()
【解析】
(1)根据题意利用旋转作图的方法画出将△ABC绕点O逆时针旋转90°所得到的![]() 以及写出
以及写出![]() 点的坐标即可;
点的坐标即可;
(2)根据题意利用作轴对称图形的方法画出将△ABC关于x轴对称的![]() 并写出
并写出![]() 点的坐标即可;
点的坐标即可;
(3)由题意可知OA扫过的图形是一个以OA长为半径的四分之一的圆,求出这个四分之一的圆即可求出线段OA扫过的图形的面积.
解:(1)如图:
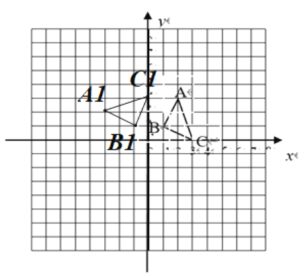
由图像可得![]() 的坐标为(-3,2);
的坐标为(-3,2);
(2)如图:

由图像可得![]() 的坐标为(2,-3);
的坐标为(2,-3);
(3)由题意可知OA扫过的图形是一个以OA长为半径的四分之一的圆,
已知A(2,3),利用勾股定理求得OA= ![]() ,
,
所以线段OA扫过的图形的面积为:![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校的学生除了体育课要进行体育锻炼外,寒暑假期间还要自己抽时间进行体育锻炼,为了了解同学们假期体育锻炼的情况,开学时体育老师随机抽取了部分同学进行调查,按锻炼的时间x(分钟)分为以下四类:A类(![]() ),B类(
),B类(![]() ),C类(
),C类(![]() ),D类(
),D类(![]() ),对调查结果进行整理并绘制了如图所示的不完整的折线统计图和扇形统计图,请结合图中的信息解答下列各题:
),对调查结果进行整理并绘制了如图所示的不完整的折线统计图和扇形统计图,请结合图中的信息解答下列各题:
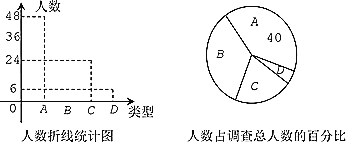
(1)扇形统计图中D类所对应的圆心角度数为 ,并补全折线统计图;
(2)现从A类中选出两名男同学和三名女同学,从以上五名同学中随机抽取两名同学进行采访,请利用画树状图或列表的方法求出抽到的学生恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)填空:![]() ,
,![]() .
.
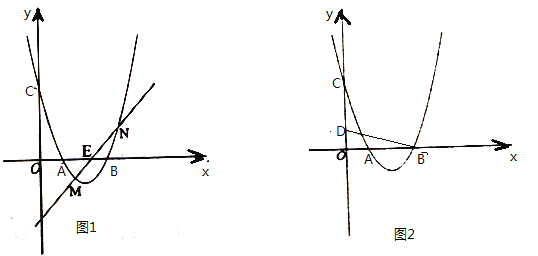
(2)如图1,已知![]() ,过点
,过点![]() 的直线与抛物线交于点
的直线与抛物线交于点![]() 、
、![]() ,且点
,且点![]() 、
、![]() 关于点
关于点![]() 对称,求直线
对称,求直线![]() 的解析式.
的解析式.
(3)如图2,已知![]() ,
,![]() 是第一象限内抛物线上一点,作
是第一象限内抛物线上一点,作![]() 轴于点
轴于点![]() ,若
,若![]() 与
与![]() 相似,请求出点
相似,请求出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据报道,“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.某校学生会想知道学生对这个提议的了解程度,随机抽取部分学生进行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题.
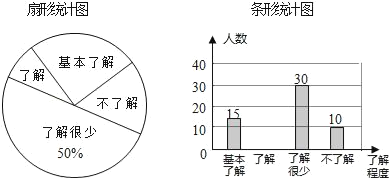
(1)接受问卷调查的学生共有 名,扇形统计图中“基本了解”部分所对应扇形的圆心角为 ;请补全条形统计图;
(2)若该校共有学生1200人,请根据上述调查结果,估计该校学生中对将“剪刀石头布”作为奥运会比赛项目的提议达到“了解””和“基本了解”程度的总人数;
(3)“剪刀石头布”比赛时双方每次任意出“剪刀”、“石头”、“布”这三种手势中的一种,规则为:剪刀胜布,布胜石头,石头胜剪刀,若双方出现相同手势,则算打平.若小刚和小明两人只比赛一局,请用树状图或列表法求两人打平的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经销一种成本为10元的产品,经市场调查发现,在一段时间内,销售量![]() (件)与销售单价
(件)与销售单价![]() ( 元/件 )的关系如下表:
( 元/件 )的关系如下表:
|
| 15 | 20 | 25 | 30 |
|
|
| 550 | 500 | 450 | 400 |
|
设这种产品在这段时间内的销售利润为![]() (元),解答下列问题:
(元),解答下列问题:
(1)如![]() 是
是![]() 的一次函数,求
的一次函数,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)求销售利润![]() 与销售单价
与销售单价![]() 之间的函数关系式;
之间的函数关系式;
(3)求当![]() 为何值时,
为何值时,![]() 的值最大?最大是多少?
的值最大?最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全教育,某校组织了“防溺水”知识竞赛,对表现优异的班级进行奖励,学校购买了若干副乒乓球拍和羽毛球拍,购买2副乒乓球拍和1副羽毛球拍共需116元;购买3幅乒乓球拍和2幅羽毛球拍共需204元.
(1)求购买1副乒乓球拍和1副羽毛球拍各需多少元;
(2)若学校购买乒乓球拍和羽毛球拍共30幅,且支出不超过1480元,则最多能够购买多少副羽毛球拍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点A(8,0)和点B(0,6),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点P的坐标是_____.
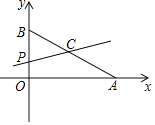
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为l的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.
(1)求证:![]() ;
;
(2)过点E作![]() 交PB于点F,连结AF,当
交PB于点F,连结AF,当![]() 时,①求证:四边形AFEP是平行四边形;
时,①求证:四边形AFEP是平行四边形;
②请判断四边形AFEP是否为菱形,并说明理由.
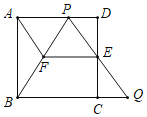
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,给出如下定义:若点
中,给出如下定义:若点![]() 在图形
在图形![]() 上,点
上,点![]() 在图形
在图形![]() 上,如果
上,如果![]() 两点间的距离有最小值,那么称这个最小值为图形
两点间的距离有最小值,那么称这个最小值为图形![]() 的“近距离”,记为
的“近距离”,记为![]() .特别地,当图形
.特别地,当图形![]() 与图形
与图形![]() 有公共点时,
有公共点时,![]() .
.
已知![]() ,
,![]() ,
,![]() ,
,
(1)![]() 点
点![]() ,点
,点![]()
![]() ,
,![]() 点
点![]() ,线段
,线段![]()
![]() ;
;
(2)⊙![]() 半径为
半径为![]() ,
,
①当![]() 时,求⊙
时,求⊙![]() 与线段
与线段![]() 的“近距离”
的“近距离”![]() ⊙
⊙![]() ,线段
,线段![]() ;
;
②若![]() ⊙
⊙![]() ,
,![]()
![]() ,则
,则![]() .
.
(3)![]() 为
为![]() 轴上一点,⊙
轴上一点,⊙![]() 的半径为1,点
的半径为1,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,⊙
,⊙![]() 与
与![]() 的“近距离”
的“近距离”![]() ⊙
⊙![]() ,
,![]() ,请直接写出圆心
,请直接写出圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com