
ЁОЬтФПЁПдФЖСВФСЯ
ВФСЯ1ЃКЖдГЦЃЌвВаэЪЧжаЙњШЫзюЯВЛЖЕФЁЃНЈжўЪІСКЫМГЩдјЫЕЙ§ЃКЁАЮоТлЖЋЗНЁЂЮїЗНЃЌдйУЛгавЛИіУёзхЖджажсЖдГЦЯпШчДЫжгАЎгыуЁЪиЁЃЁБЗХблжаЙњЕФНЈжўЃЌЮоТлЪЧЙЌЕюЁЂУэгюЁЂЭЄЬЈЁЂТЅИѓЁЂдАСжЮоВЛгазХЖдГЦжЎУРЁЃЪ§бЇЪРНчвВРягавЛаЉе§ећЪ§ФуЮоТлДгзѓЭљгвПДЃЌЛЙЪЧДггвЭљзѓПДЃЌЪ§зжЖМЪЧЭъШЋвЛбљЕФЃЌР§ШчЃК11ЁЂ101ЁЂ2332ЁЂ1234321ЁЂЁЃЌЯёетбљЕФЪ§ЮвУЧНаЫќЁАЖдГЦЪ§ЁБЃЎ
ВФСЯ2ЃКШчЙћвЛИіШ§ЮЛЪ§![]() ЃЌТњзуa+b+cЃН8ЃЌЮвУЧОЭГЦетИіШ§ЮЛЪ§ЮЊЁАЗЂВЦЪ§ЁБЃЎ
ЃЌТњзуa+b+cЃН8ЃЌЮвУЧОЭГЦетИіШ§ЮЛЪ§ЮЊЁАЗЂВЦЪ§ЁБЃЎ
ЃЈ1ЃЉЧыжБНгаДГіМШЪЧЁАЖдГЦЪ§ЁБгжЪЧЁАЗЂВЦЪ§ЁБЕФЫљгаШ§ЮЛЪ§ЃЛ
ЃЈ2ЃЉвЛИіШ§ЮЛЁАЖдГЦЪ§ЁБЪЎЮЛЪ§зжЮЊ7ЃЌЫќЕФИїЪ§ЮЛЩЯЕФЪ§зжжЎКЭЪЧвЛИіздШЛЪ§ЕФЦНЗНЃЌЧѓетИіШ§ЮЛЪ§ЃЈЧыаДГіБивЊЕФЭЦРэЙ§ГЬЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉ161ЃЌ242ЃЌ323ЃЌ404ЃЛЃЈ2ЃЉ171ЃЌ979ЃЌ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЁАЖдГЦЪ§ЁБКЭЁАЗЂВЦЪ§ЁБЕФЖЈвхМДПЩаДГіЃЛ
ЃЈ2ЃЉЩшетИіШ§ЮЛЁАЖдГЦЪ§ЁБЮЊ![]() ЃЈxЮЊ1-9ЕФздШЛЪ§ЃЉЃЌЙЪx+7+x=2x+7ЃЌгЩxЮЊ1-9ЕФздШЛЪ§ПЩЕУЕН2x+7ЕФШЁжЕЗЖЮЇЃЌдйИљОнИїЪ§ЮЛЩЯЕФЪ§зжжЎКЭЪЧвЛИіздШЛЪ§ЕФЦНЗНЃЌЕУЕН2x+7ПЩФмЕФжЕЃЌдйНјааЧѓНтМДПЩ.
ЃЈxЮЊ1-9ЕФздШЛЪ§ЃЉЃЌЙЪx+7+x=2x+7ЃЌгЩxЮЊ1-9ЕФздШЛЪ§ПЩЕУЕН2x+7ЕФШЁжЕЗЖЮЇЃЌдйИљОнИїЪ§ЮЛЩЯЕФЪ§зжжЎКЭЪЧвЛИіздШЛЪ§ЕФЦНЗНЃЌЕУЕН2x+7ПЩФмЕФжЕЃЌдйНјааЧѓНтМДПЩ.
ЃЈ1ЃЉМШЪЧЁАЖдГЦЪ§ЁБгжЪЧЁАЗЂВЦЪ§ЁБЕФЫљгаШ§ЮЛЪ§га161ЃЌ242ЃЌ323ЃЌ404ЃЛ
ЃЈ2ЃЉЩшетИіШ§ЮЛЁАЖдГЦЪ§ЁБЮЊ![]() ЃЈxЮЊ1-9ЕФздШЛЪ§ЃЉЃЌ
ЃЈxЮЊ1-9ЕФздШЛЪ§ЃЉЃЌ
ЙЪx+7+x=2x+7ЃЌ
ЁпxЮЊ1-9ЕФздШЛЪ§
Ёр2x+7ЕФШЁжЕЗЖЮЇЮЊ9Ём2x+7Ём25ЃЌ
ЁпИїЪ§ЮЛЩЯЕФЪ§зжжЎКЭЪЧвЛИіздШЛЪ§ЕФЦНЗНЃЌ
Ёр2x+7ПЩФмЕФжЕЮЊ9,16,25ЃЌ
ЙЪЕБ2x+7=9ЪБЃЌНтЕУx=1, етИіШ§ЮЛЁАЖдГЦЪ§ЁБЮЊ171ЃЛ
ЕБ2x+7=16ЪБЃЌНтЕУx=![]() , етИіШ§ЮЛЁАЖдГЦЪ§ЁБВЛДцдкЃЛ
, етИіШ§ЮЛЁАЖдГЦЪ§ЁБВЛДцдкЃЛ
ЕБ2x+7=25ЪБЃЌНтЕУx=9, етИіШ§ЮЛЁАЖдГЦЪ§ЁБЮЊ979ЃЛ
злЩЯЃКетИіШ§ЮЛЪ§ЮЊ171Лђ979.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ12ЗжЃЉФГБіЙнзМБИЙКНјвЛХњЛЛЦјЩШЃЌДгЕчЦїЩЬГЁСЫНтЕНЃКвЛЬЈAаЭЛЛЦјЩШКЭШ§ЬЈBаЭЛЛЦјЩШЙВаш275дЊЃЛШ§ЬЈAаЭЛЛЦјЩШКЭЖўЬЈBаЭЛЛЦјЩШЙВаш300дЊЃЎ
ЃЈ1ЃЉЧѓвЛЬЈAаЭЛЛЦјЩШКЭвЛЬЈBаЭЛЛЦјЩШЕФЪлМлИїЪЧЖрЩйдЊЃЛ
ЃЈ2ЃЉШєИУБіЙнзМБИЭЌЪБЙКНјетСНжжаЭКХЕФЛЛЦјЩШЙВ40ЬЈВЂЧвAаЭЛЛЦјЩШЕФЪ§СПВЛЖргкBаЭЛЛЦјЩШЪ§СПЕФ3БЖЃЌЧыЩшМЦГізюЪЁЧЎЕФЙКТђЗНАИЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЦНааЫФБпаЮABCDжаЃЌADЁЮBCЃЌЙ§BзїBEЁЭADНЛADгкЕуEЃЌABЃН13cmЃЌBCЃН21cmЃЌAEЃН5cmЃЎЖЏЕуPДгЕуCГіЗЂЃЌдкЯпЖЮCBЩЯвдУПУы1cmЕФЫйЖШЯђЕуBдЫЖЏЃЌЖЏЕуQЭЌЪБДгЕуAГіЗЂЃЌдкЯпЖЮADЩЯвдУПУы2cmЕФЫйЖШЯђЕуDдЫЖЏЃЌЕБЦфжавЛИіЖЏЕуЕНДяЖЫЕуЪБСэвЛИіЖЏЕувВЫцжЎЭЃжЙдЫЖЏЃЌЩшдЫЖЏЕФЪБМфЮЊt(Уы)
(1)ЕБtЮЊКЮжЕЪБЃЌЫФБпаЮPCDQЪЧЦНааЫФБпаЮЃП
(2)ЕБtЮЊКЮжЕЪБЃЌЁїQDPЕФУцЛ§ЮЊ60cm2ЃП
(3)ЕБtЮЊКЮжЕЪБЃЌPDЃНPQЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПУнЕФдЫЫуЃК
ЃЈ1ЃЉМЦЫуЃКЃЈЉa3ЃЉ2+ЃЈЉa2ЃЉ3
ЃЈ2ЃЉМЦЫуЃК![]()
ЃЈ3ЃЉ![]()
ЃЈ4ЃЉЮвУЧвбОбЇЯАСЫЫФИіЙигкУнЕФдЫЫуЗЈдђЃКЂйamanЃНam+nЃЛЂкЃЈamЃЉnЃНamnЃЛЂлЃЈabЃЉmЃНambmЃЛЂмamЁТanЃНamЉnЃЌЯТУцЪЧаЁУїМЦЫуЕФЙ§ГЬЃЈa3a2ЃЉ3ЃНЃЈa3+2ЃЉ3ЃНЃЈa5ЃЉ3ЃНa15ЃЌЫћгУЕНЕФЙЋЪНгаЁЁ ЃЈЬюађКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьЯТСаСНИіЕШЪНЃК![]() ЃЌ
ЃЌ![]() ЃЌИјГіЖЈвхШчЯТЃКЮвУЧГЦЪЙЕШЪН
ЃЌИјГіЖЈвхШчЯТЃКЮвУЧГЦЪЙЕШЪН![]() ГЩСЂЕФвЛЖдгаРэЪ§
ГЩСЂЕФвЛЖдгаРэЪ§![]() ЮЊЁАРэЯыгаРэЪ§ЖдЁБЃЌМЧЮЊ
ЮЊЁАРэЯыгаРэЪ§ЖдЁБЃЌМЧЮЊ![]() ЃЌШчЃКЪ§Жд
ЃЌШчЃКЪ§Жд![]() ЁЂ
ЁЂ![]() ЖМЪЧЁАРэЯыгаРэЪ§ЖдЁБ.
ЖМЪЧЁАРэЯыгаРэЪ§ЖдЁБ.
ЃЈ1ЃЉЪ§Жд![]() ЁЂ
ЁЂ![]() жаЪЧЁАРэЯыгаРэЪ§ЖдЁБЕФЪЧ______ЃЛ
жаЪЧЁАРэЯыгаРэЪ§ЖдЁБЕФЪЧ______ЃЛ
ЃЈ2ЃЉШє![]() ЪЧЁАРэЯыгаРэЪ§ЖдЁБЃЌЧѓaЕФжЕЃЛ
ЪЧЁАРэЯыгаРэЪ§ЖдЁБЃЌЧѓaЕФжЕЃЛ
ЃЈ3ЃЉШє![]() ЪЧЁАРэЯыгаРэЪ§ЖдЁБЃЌдђ
ЪЧЁАРэЯыгаРэЪ§ЖдЁБЃЌдђ![]() ______ЁАРэЯыгаРэЪ§ЖдЁБЃЈЬюЁАЪЧЁБЁЂЁАВЛЪЧЁБЛђЁАВЛШЗЖЈЁБЃЉЃЛ
______ЁАРэЯыгаРэЪ§ЖдЁБЃЈЬюЁАЪЧЁБЁЂЁАВЛЪЧЁБЛђЁАВЛШЗЖЈЁБЃЉЃЛ
ЃЈ4ЃЉЧыдйаДГівЛЖдЗћКЯЬѕМўЕФЁАРэЯыгаРэЪ§ЖдЁБ.ЃЈВЛФмгыЬтФПжавбгаЕФЪ§ЖджиИДЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПећЪНГЫЗЈКЭГЫЗЈЙЋЪН
ЃЈ1ЃЉМЦЫуЃКЃЈЉxЃЉ2ЃЈ2yЃЉ3
ЃЈ2ЃЉЛЏМђЃКЃЈa+1ЃЉ2+2ЃЈaЉ1ЃЉЃЈa+1ЃЉ+ЃЈaЉ1ЃЉ2
ЃЈ3ЃЉШчЙћЃЈx+1ЃЉЃЈx2+ax+bЃЉЕФГЫЛ§жаВЛКЌx2ЯюКЭxЯюЃЌЧѓЯТУцЪНзгЕФжЕЃКЃЈa+2bЃЉЃЈa+bЃЉЉ2ЃЈa+bЃЉ2
ЃЈ4ЃЉПЮБОЩЯЃЌЙЋЪНЃЈaЉbЃЉ2ЃНa2Љ2ab+b2ЪЧгЩЙЋЪНЃЈa+bЃЉ2ЃНa2+2ab+b2ЭЦЕМЕУГіЕФЃЌвбжЊЃЈa+bЃЉ3ЃНa3+3a2b+3ab2+b3ЃЌдђЃЈaЉbЃЉ3ЃНЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИљОнЯТУцИјГіЕФЪ§жсЃЌНтД№ЯТУцЕФЮЪЬтЃК
![]()
ЃЈ1ЃЉЧыФуИљОнЭМжаAЁЂBСНЕуЕФЮЛжУЃЌЗжБ№аДГіЫќУЧЫљБэЪОЕФгаРэЪ§AЃКЁЁ ,BЃКЁЁ ЃЛ
ЃЈ2ЃЉЙлВьЪ§жсЃЌгыЕуAЕФОрРыЮЊ4ЕФЕуБэЪОЕФЪ§ЪЧЃКЁЁ ЁЁЃЛ
ЃЈ3ЃЉШєНЋЪ§жселЕўЃЌЪЙЕУAЕугыЉ3БэЪОЕФЕужиКЯЃЌдђBЕугыЪ§ЁЁ БэЪОЕФЕужиКЯЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇаЃзщжЏжаЙњЙВВњЕГЕкЪЎОХДЮШЋЙњДњБэДѓЛсжЊЪЖЮЪД№ЃЌЙВЩшга20ЕРбЁдёЬтЃЌИїЬтЗжжЕЯрЭЌЃЌУПЬтБиД№.ЯТБэМЧТМСЫAЁЂBЁЂDШ§УћВЮШќбЇЩњЕФЕУЗжЧщПіЃК
ВЮШќбЇЩњ | Д№ЖдЬтЪ§ | Д№ДэЬтЪ§ | ЕУЗж |
A | 20 | 0 | 100 |
B | 19 | 1 | 94 |
D | 14 | 6 | 64 |
дђВЮШќбЇЩњEЕФЕУ ЗжПЩФм ЪЧ( )
A.93B.87C.66D.40
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
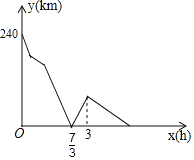
ЁОЬтФПЁПМзЁЂввСНГЕЗжБ№ДгЯрОр240ЧЇУзЕФAЃЌBСНЕиЭЌЪБЯрЯђдШЫйГіЗЂЃЌМзГЕГіЗЂ0.5аЁЪБКѓЗЂЯжгаЖЋЮїТфдкГіЗЂЕиAЕиЃЌгкЪЧСЂМДАДдЫйбидТЗЗЕЛиЃЌдкAЕиШЁЕНЖЋЮїКѓСЂМДвддЫйМЬајЯђBЕиааЪЛЃЌВЂдкЭОжагыввГЕЕквЛДЮЯргіЃЌЯргіКѓМзЁЂввСНГЕМЬајвдИїздЕФЫйЖШГЏзХИїздЕФЗНЯђдШЫйааЪЛЃЌЕБввГЕЕНДяAЕиКѓЃЌСЂМДЕєЭЗвддЫйПЊЭљBЕиЃЈМзГЕШЁЖЋЮїЁЂЕєЭЗКЭввГЕЕєЭЗЕФЪБМфОљКіТдВЛМЦЃЉЃЎСНГЕжЎМфЕФОрРыyЃЈЧЇУзЃЉгыМзГЕГіЗЂЕФЪБМфxЃЈаЁЪБЃЉжЎМфЕФВПЗжЙиЯЕШчЭМЫљЪОЃЌдђЕБввГЕЕНДяBЕиЪБЃЌМзГЕгыBЕиЕФОрРыЮЊ_____ЧЇУзЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com