
【题目】如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由.

【答案】(1)y=![]() ﹣1;(2) △ABM为直角三角形.理由详见解析.
﹣1;(2) △ABM为直角三角形.理由详见解析.
【解析】
试题分析:(1)由条件可分别求得A、B的坐标,设出抛物线解析式,利用待定系数法可求得抛物线解析式;
(2)结合(1)中A、B、C的坐标,根据勾股定理可分别求得AB、AM、BM,可得到![]() ,可判定△ABM为直角三角形.
,可判定△ABM为直角三角形.
试题解析:(1)∵A点为直线y=x+1与x轴的交点,
∴A(﹣1,0),
又B点横坐标为2,代入y=x+1可求得y=3,
∴B(2,3),
∵抛物线顶点在y轴上,
∴可设抛物线解析式为y=![]() +c,
+c,
把A、B两点坐标代入可得![]() ,
,
解得![]() ,
,
∴抛物线解析式为y=![]() ﹣1;
﹣1;
(2)△ABM为直角三角形.理由如下:
由(1)抛物线解析式为y=![]() ﹣1,可知M点坐标为(0,﹣1),
﹣1,可知M点坐标为(0,﹣1),
∴![]() =2,
=2,![]() =18,
=18,![]() =20,
=20,
∴![]() ,
,
∴△ABM为直角三角形.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连接AP交BC于点E,连接BP交AC于点F. 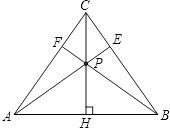
(1)证明:∠CAE=∠CBF;
(2)证明:AE=BF;
(3)以线段AE,BF和AB为边构成一个新的三角形ABG(点E与点F重合于点G),记△ABC和△ABG的面积分别为S△ABC和S△ABG , 如果存在点P,能使得S△ABC=S△ABG , 求∠ACB的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】a是不为1的有理数,我们把 ![]() 称为a的差倒数.如:2的差倒数是
称为a的差倒数.如:2的差倒数是 ![]() =﹣1,﹣1的差倒数是
=﹣1,﹣1的差倒数是 ![]() =
= ![]() .已知a1=
.已知a1= ![]() ,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2016= .
,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2016= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红设计了如图所示的一个计算程序: ![]()
根据这个程序解答下列问题:
(1)若小刚输入的数为﹣4,则输出结果为 ,
(2)若小红的输出结果为123,则她输入的数为 ,
(3)这个计算程序可列出算式为 , 计算结果为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列各式中,应填入“(-y)”的是( )
A. -y3·______=-y4 B. 2y3·______=-2y4
C. (-2y)3·______=-8y4 D. (-y)12·______=-3y13
查看答案和解析>>
科目:初中数学 来源: 题型:
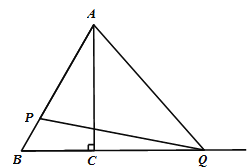
【题目】如图,在△ABC中,∠ACB=90°, ∠ABC=60°,BC=6.动点P从点A出发沿AB方向以每秒2个单位的速度运动,同时动点Q从点C出发沿射线BC方向以每秒2个单位的速度运动,当点P到达点B时,P、Q同时停止运动,连结PQ、QA.设点P运动的时间为t秒.
(1)当CQ=2BP时,求t的值;
(2)当t为何值时QP=QA;
(3)若线段PQ的中垂线与线段BC相交(包括线段的端点),则t的取值范围是 .(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com