
分析 (1)设公司建甲种户型x套,则B种户型(80-x)套,根据该公司所用建房资金不少于2850万元,列出不等式,进行求解即可;
(2)设所获得利润为W万元,根据一套的利润×总的套数=总利润,列出一次函数,再根据函数的增减性即可得出答案;
(3)分两种情况讨论:当0<a<1和1<a<1.5时,分别得出甲住房和乙住房各多少套时,该公司才能获得最大利润.
解答 解:(1)设公司建甲种户型x套,则B种户型(80-x)套,
45x+30(80-x)≥2850
解得:x≥30,
答:公司最少建甲种户型30套;
(2)设所获得利润为W万元,根据题意得:
W=(51-45)x+(35-30)(80-x)
=x+400,
∵k=1>0,
∴W随x的增大而增大,
∴当x取最大值32时,W有最大值432万元;
(3)当0<a<1时,甲住房有32套,乙住房有48套,该公司才能获得最大利润;
当1<a<1.5时,甲住房有30套,乙住房有50套,该公司才能获得最大利润;
点评 此题考查了一元一次不等式的应用和一次函数的应用,读懂题意,找出它们之间的数量关系,列出不等式或一次函数,掌握函数的增减性是解题的关键.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:初中数学 来源: 题型:解答题
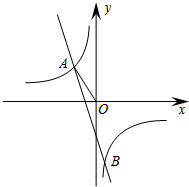 已知反比例函数y=$\frac{k_1}{3x}$的图象与一次函数y=k2x+m的图象交于A(a,1)、B($\frac{1}{3}$,-3)两点,连结AO.
已知反比例函数y=$\frac{k_1}{3x}$的图象与一次函数y=k2x+m的图象交于A(a,1)、B($\frac{1}{3}$,-3)两点,连结AO.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
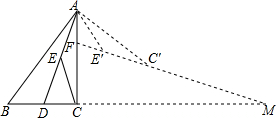 在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AD平分∠CAB交BC于点D,E为AD的中点,连接CE,将△ACE绕点A逆时针旋转至△AE′C′,直线E′C′交AC于点F,交BC的延长线于点M,若AF=E′F,则CM=$\frac{96-10\sqrt{10}}{7}$.
在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AD平分∠CAB交BC于点D,E为AD的中点,连接CE,将△ACE绕点A逆时针旋转至△AE′C′,直线E′C′交AC于点F,交BC的延长线于点M,若AF=E′F,则CM=$\frac{96-10\sqrt{10}}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 要消去y,可以将①×5+②×2 | B. | 要消去x,可以将①×3+②×(-5) | ||
| C. | 要消去y,可以将①×5+②×3 | D. | 要消去x,可以将①×(-5)+②×2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
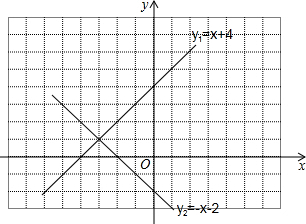 在同一平面直角坐标系内画直线y1=x+4和y2=-x-2图象,根据图象回答:
在同一平面直角坐标系内画直线y1=x+4和y2=-x-2图象,根据图象回答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 距离地面高度h/km | 0 | 1 | 2 | 3 | 4 | 5 | … |
| 温度T/℃ | 20 | 14 | 8 | 2 | -4 | -10 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
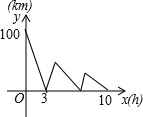 甲、乙两车分别从A、B两地同时出发,相向而行,甲车从A地行驶到B地后,立即按原速度返回A地,乙车从B地行驶到A地,两车到达A地均停止运动.两车之间的距离y(单位:千米)与乙车行驶时间x(单位:小时)之间的函数关系如图所示,问两车第二次相遇时乙车行驶的时间为$\frac{15}{2}$小时.
甲、乙两车分别从A、B两地同时出发,相向而行,甲车从A地行驶到B地后,立即按原速度返回A地,乙车从B地行驶到A地,两车到达A地均停止运动.两车之间的距离y(单位:千米)与乙车行驶时间x(单位:小时)之间的函数关系如图所示,问两车第二次相遇时乙车行驶的时间为$\frac{15}{2}$小时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com