
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B、C重合),过点C作CN垂直DM交AB于点N,连结OM、ON、MN.下列五个结论:①△CNB≌△DMC;②![]() ;③ON⊥OM;④若AB=2,则
;③ON⊥OM;④若AB=2,则![]() 的最小值是1;⑤
的最小值是1;⑤![]() .其中正确结论是_________.(只填番号)
.其中正确结论是_________.(只填番号)

【答案】①②③⑤
【解析】根据正方形的性质,依次判定△CNB≌△DMC,△OCM≌△OBN,△CON≌△DOM,根据全等三角形的性质以及勾股定理进行计算即可得出结论.
∵正方形ABCD中,CD=BC,∠BCD=90°,
∴∠BCN+∠DCN=90°,
又∵CN⊥DM,
∴∠CDM+∠DCN=90°,
∴∠BCN=∠CDM,
又∵∠CBN=∠DCM=90°,
∴△CNB≌△DMC(ASA),故①正确;
根据△CNB≌△DMC,可得CM=BN,
又∵∠OCM=∠OBN=45°,OC=OB,
∴△OCM≌△OBN(SAS),
∴OM=ON,故②正确;
∵△OCM≌△OBN
∴∠COM=∠BON
∴∠COM+∠BOM=∠BON+∠BOM=90°
∴ON⊥OM
故③正确;
∵△OCM≌△OBN,
∴四边形BMON的面积=△BOC的面积=1,即四边形BMON的面积是定值1,
∴当△MNB的面积最大时,△MNO的面积最小,
设BN=x=CM,则BM=2-x,
∴△MNB的面积=![]() x(2-x)=-
x(2-x)=-![]() x2+x,
x2+x,
∴当x=1时,△MNB的面积有最大值![]() ,
,
此时S△OMN的最小值是1-![]() =
=![]() ,故④不正确;
,故④不正确;
∵AB=BC,CM=BN,
∴BM=AN,
又∵Rt△BMN中,BM2+BN2=MN2,
∴AN2+CM2=MN2,故⑤正确;


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
【题目】综合题。
(1)计算:(π﹣3.14)0+( ![]() )﹣1+|﹣2
)﹣1+|﹣2 ![]() |﹣
|﹣ ![]() .
.
(2)先化简,再求值: ![]() ÷(
÷( ![]() ﹣x+1),并从﹣tan60°≤x≤2cos30°取出一个合适的整数,求出式子的值.
﹣x+1),并从﹣tan60°≤x≤2cos30°取出一个合适的整数,求出式子的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
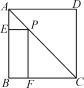
【题目】如图,P为正方形ABCD的对角线AC上任意一点,PE⊥AB于E,PF⊥BC于F,若AC=![]() ,则四边形PEBF的周长为( )
,则四边形PEBF的周长为( )
A. ![]() B. 2
B. 2![]() C. 2 D. 1
C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于C、D两点,与反比例函数
轴交于C、D两点,与反比例函数![]() 的图像相交于点
的图像相交于点![]() 和点
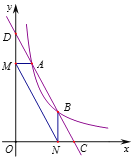
和点![]() ,过点A作AM⊥y轴于点M,过点B作BN⊥x轴于点N,连结MN、OA、OB.下列结论:
,过点A作AM⊥y轴于点M,过点B作BN⊥x轴于点N,连结MN、OA、OB.下列结论:
①![]() ;②
;②![]() ;③四边形
;③四边形![]() 与四边形MNCA的周长相等;④
与四边形MNCA的周长相等;④![]() .其中正确的个数是( )个.
.其中正确的个数是( )个.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在反比例函数y= ![]() (x>0)的图象上有点P1、P2、P3、P4 , P5 , 它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , S4 , 则S1+S2+S3+S4的值为( )
(x>0)的图象上有点P1、P2、P3、P4 , P5 , 它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , S4 , 则S1+S2+S3+S4的值为( ) 
A.4.5
B.4.2
C.4
D.3.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒2°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒4°的速度旋转,如图2,设旋转时间为t(0秒≤t≤90秒).
(1)用含t的代数式表示∠MOA的度数.
(2)在运动过程中,当∠AOB第二次达到60°时,求t的值.
(3)在旋转过程中是否存在这样的t,使得射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请直接写出t的值;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
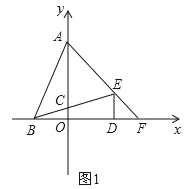
【题目】如图,在平面直角坐标系中,点A(0,b)、B(a,0)、D(d,0),且a、b、d满足![]() =0,DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F
=0,DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F
(1)求点A、B、D的坐标;
(2)求点E、F的坐标;
(3)如图,点P(0,1)作x轴的平行线,在该平行线上有一点Q(点Q在点P的右侧)使∠QEM=45°,QE交x轴于点N,ME交y轴的正半轴于点M,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
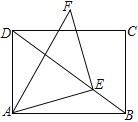
【题目】如图,矩形ABCD中,AB=4,AD=3,E为对角线BD上一个动点,以E为直角顶点,AE为直角边作等腰Rt△AEF,A、E、F按逆时针排列.当点E从点B运动到点D时,点F的运动路径长为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com