
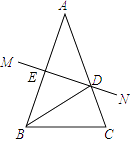
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E. 
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求△ABC的周长.
【答案】
(1)解:∵在△ABC中,AB=AC,∠A=40°,
∴∠ABC=∠C=70°,
∵AB的垂直平分线MN交AC于点D,
∴AD=BD,
∴∠ABD=∠A=40°,
∴∠DBC=∠ABC﹣∠ABD=30°
(2)解:∵MN垂直平分AB,
∴DA=DB,
∵BC+BD+DC=20,
∴AD+DC+BC=20,
∴AC+BC=20,
∵AB=2AE=12,
∴△ABC的周长=AB+AC+BC=12+20=32.
【解析】(1)由在△ABC中,AB=AC,∠A=42°,利用等腰三角形的性质,即可求得∠ABC的度数,然后由AB的垂直平分线MN交AC于点D,根据线段垂直平分线的性质,可求得AD=BD,继而求得∠ABD的度数,则可求得∠DBC的度数.(2)由△CBD的周长为20,推出AC+BC=20,根据AB=2AE=12,由此即可解决问题.
【考点精析】本题主要考查了线段垂直平分线的性质和等腰三角形的性质的相关知识点,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①点P在∠A的角平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.正确的有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°. 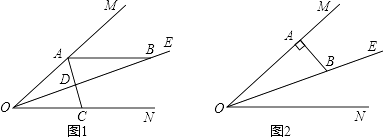
(1)如图1,若AB∥ON,则
①∠ABO的度数是;
②当∠BAD=∠ABD时,x=;当∠BAD=∠BDA时,x= .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0; ②b>a+c;③9a+3b+c>0;④c<-3a;⑤a+b+c≥m(am+b)+c,其中正确的有( )个。

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com