

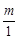 ,即m=2。
,即m=2。
|
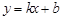 ,由点A(1,0),点B(2,1)在
,由点A(1,0),点B(2,1)在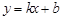 上,得
上,得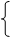 , ,解之,得
, ,解之,得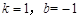
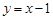 。
。 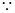 点P(a,a-1)(a>1)在直线y=2上, ∴P(3,2)
点P(a,a-1)(a>1)在直线y=2上, ∴P(3,2)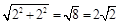 , BP=
, BP=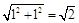
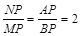


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源:不详 题型:解答题
 与一次函数y=-x+2的图象交于A、B两点,且点A的横坐标是-2.
与一次函数y=-x+2的图象交于A、B两点,且点A的横坐标是-2.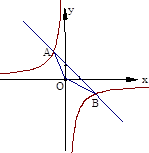
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
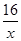 (x>0)的图象上,
(x>0)的图象上,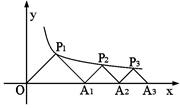
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图像过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.
的图像过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13. 和直线OE的函数解析式;
和直线OE的函数解析式;
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点
的图像上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点 在第二象限;
在第二象限; ,并写出点
,并写出点 的坐标;
的坐标; M的解析式y﹦kx+b进行探究:
M的解析式y﹦kx+b进行探究: 和点M的坐标.
和点M的坐标.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象交于点
的图象交于点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com