
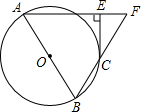
 如图,AB为⊙O的直径,AE⊥CE于点E,BC的延长线与AE的延长线相交于点F.若CE为⊙O的切线,AF=BF,求∠A的度数.
如图,AB为⊙O的直径,AE⊥CE于点E,BC的延长线与AE的延长线相交于点F.若CE为⊙O的切线,AF=BF,求∠A的度数. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
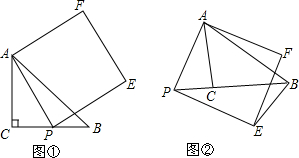
 如图,是某校美术室的一个道具,它是由棱长均为10dm的小立方块搭成的,工人师傅要将其表面(底面除外)涂上油漆,请你计算一下,工人师傅至少需涂多少平方米的油漆?
如图,是某校美术室的一个道具,它是由棱长均为10dm的小立方块搭成的,工人师傅要将其表面(底面除外)涂上油漆,请你计算一下,工人师傅至少需涂多少平方米的油漆?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{5}$和5 | B. | 8和-(-8) | C. | -2.5和2$\frac{1}{2}$ | D. | $\frac{1}{3}$和0.333 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个三角形中至少有两个锐角 | |
| B. | 一个三角形中,一个外角大于任意一个内角 | |
| C. | 三角形的外角和等于360° | |
| D. | 锐角三角形,任何两个内角的和均大于90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com