
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=ax2+3x½»xÖįÕż°ėÖįÓŚµćA£Ø6£¬0£©£¬¶„µćĪŖM£¬¶Ō³ĘÖįMB½»xÖįÓŚµćB£¬¹żµćC£Ø2£¬0£©×÷ÉäĻßCD½»MBÓŚµćD£ØDŌŚxÖįÉĻ·½£©£¬OE”ĪCD½»MBÓŚµćE£¬EF”ĪxÖį½»CDÓŚµćF£¬×÷Ö±ĻßMF£®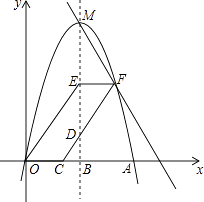
£Ø1£©ĒóaµÄÖµ¼°MµÄ×ų±ź£»
£Ø2£©µ±BDĪŖŗĪÖµŹ±£¬µćFĒ”ŗĆĀäŌŚøĆÅ×ĪļĻßÉĻ£æ
£Ø3£©µ±”ĻDCB=45”揱£ŗ
¢ŁĒóÖ±ĻßMFµÄ½āĪöŹ½£»
¢ŚŃÓ³¤OE½»FMÓŚµćG£¬ĖıߊĪDEGFŗĶĖıߊĪOEDCµÄĆ껿·Ö±š¼ĒĪŖS1”¢S2 £¬ ŌņS1£ŗS2µÄÖµĪŖ£ØÖ±½ÓŠ““š°ø£©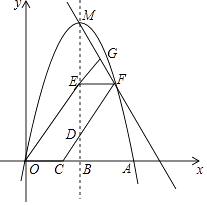
”¾“š°ø”æ
£Ø1£©½ā£ŗ°ŃA£Ø6£¬0£©“śČėy=ax2+3xµĆ36a+18=0£¬½āµĆa=© ![]() £»
£»
Å×ĪļĻß½āĪöŹ½ĪŖy=© ![]() x2+3x£¬
x2+3x£¬
”ßy=© ![]() £Øx©3£©2+
£Øx©3£©2+ ![]() £¬
£¬
”ąMµćµÄ×ų±źĪŖ£Ø3£¬ ![]() £©
£©
£Ø2£©½ā£ŗ”ßCF”ĪOE£¬EF”ĪOC£¬
”ąĖıߊĪOCFEĪŖĘ½ŠŠĖıߊĪ£¬
”ąEF=OC=2£¬
”ßÅ×ĪļĻߵĶŌ³ĘÖįĪŖÖ±Ļßx=3£¬B£Ø3£¬0£©£¬
”ąFµćµÄŗį×ų±źĪŖ5£¬
µ±x=5Ź±£¬y=© ![]() x2+3x=
x2+3x= ![]() £¬¼“F£Ø5£¬
£¬¼“F£Ø5£¬ ![]() £©£¬
£©£¬
”ąBE= ![]() £¬
£¬
”ßEF”ĪBC£¬
”ą”÷BCD”×”÷EFD£¬
”ą ![]() =
= ![]() =
= ![]() £¬
£¬
”ąBD= ![]() BE=
BE= ![]() ”Į
”Į ![]() =
= ![]() £¬
£¬
¼“µ±BDĪŖ ![]() Ź±£¬µćFĒ”ŗĆĀäŌŚøĆÅ×ĪļĻßÉĻ
Ź±£¬µćFĒ”ŗĆĀäŌŚøĆÅ×ĪļĻßÉĻ
£Ø3£©”ßCD”ĪOE,”ą”ĻBOE=”ĻDCB=45”改”÷BOEĪŖµČŃüÖ±½ĒČż½ĒŠĪ, ”ąBE=OE=3,ŌņE£Ø3,3£©,”ąÖ±ĻßOEµÄ½āĪöŹ½ĪŖy=x,Ķ¬ĄķæɵƔ÷BCDĪŖµČŃüÖ±½ĒČż½ĒŠĪ,”ąBD=BC=1,”ąDE=2,”ßEF”ĪOC,EF=OC=2,”ąF£Ø5,3£©,ÉčÖ±ĻßMFµÄ½āĪöŹ½ĪŖy=kx+b,°ŃM£Ø3,![]() £©,F£Ø5,3£©“śČėµĆ
£©,F£Ø5,3£©“śČėµĆ  ,½āµĆ
,½āµĆ  ,”ąÖ±ĻßMFµÄ½āĪöŹ½ĪŖy=©
,”ąÖ±ĻßMFµÄ½āĪöŹ½ĪŖy=© ![]() x+
x+ ![]() £»,
£»,![]()
”¾½āĪö”æ½ā£ŗ£Ø3£©¢Ś½ā·½³Ģ×é  µĆ
µĆ  £¬ŌņG£Ø
£¬ŌņG£Ø ![]() £¬
£¬ ![]() £©£¬
£©£¬
”ąS1=S”÷GEF+S”÷DEF= ![]() ”Į2”Į£Ø
”Į2”Į£Ø ![]() ©3£©+
©3£©+ ![]() ”Į2”Į2=
”Į2”Į2= ![]() £¬
£¬
S2=S”÷BOE©S”÷BCD= ![]() ”Į3”Į3©
”Į3”Į3© ![]() ”Į1”Į1=4£¬
”Į1”Į1=4£¬
”ą ![]() =
= ![]() =
= ![]() £®
£®
ĖłŅŌ“š°øŹĒ ![]() £®
£®
”¾æ¼µć¾«Īö”æ±¾ĢāÖ÷ŅŖæ¼²éĮĖČ·¶ØŅ»“ĪŗÆŹżµÄ±ķ“ļŹ½ŗĶ¶ž“ĪŗÆŹżµÄ×īÖµµÄĻą¹ŲÖŖŹ¶µć£¬ŠčŅŖÕĘĪÕČ·¶ØŅ»øöŅ»“ĪŗÆŹż£¬ŠčŅŖČ·¶ØŅ»“ĪŗÆŹż¶ØŅåŹ½y=kx+b£Øk²»µČÓŚ0£©ÖŠµÄ³£ŹżkŗĶb£®½āÕāĄąĪŹĢāµÄŅ»°ć·½·ØŹĒ“ż¶ØĻµŹż·Ø£»Čē¹ū×Ō±äĮæµÄȔֵ·¶Ī§ŹĒČ«ĢåŹµŹż£¬ÄĒĆ“ŗÆŹżŌŚ¶„µć“¦Č”µĆ×ī“óÖµ£Ø»ņ×īŠ”Öµ£©£¬¼“µ±x=-b/2aŹ±£¬y×īÖµ=(4ac-b2)/4a²ÅÄÜÕżČ·½ā“š“ĖĢā£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪABCDŹĒĘ½ŠŠĖıߊĪ£¬E£¬FŹĒ¶Ō½ĒĻßBDÉĻµÄµć£¬”Ļ1=”Ļ2.
ĒóÖ¤£ŗ£Ø1£©BE=DF£»£Ø2£©AF”ĪCE.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćA”¢B×ų±ź·Ö±šĪŖ£Ø0£¬4£©”¢£Ø2£¬0£©£¬µćCĪŖÖ±ĻßABÉĻŅ»µć£¬ČōBC£½3AC£¬ŌņµćCµÄ×ų±źĪŖ_____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĮāŠĪABCDÖŠ£¬tan”ĻABC= ![]() £¬PĪŖABÉĻŅ»µć£¬ŅŌPBĪŖ±ßĻņĶā×÷ĮāŠĪPMNB£¬Į¬½įDM£¬Č”DMÖŠµćE£¬Į¬½įAE£¬PE£¬Ōņ
£¬PĪŖABÉĻŅ»µć£¬ŅŌPBĪŖ±ßĻņĶā×÷ĮāŠĪPMNB£¬Į¬½įDM£¬Č”DMÖŠµćE£¬Į¬½įAE£¬PE£¬Ōņ ![]() µÄÖµĪŖ£Ø £©
µÄÖµĪŖ£Ø £©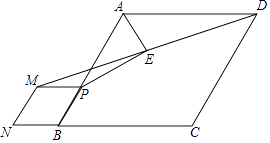
A.![]()
B.![]()
C.![]()
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷ABCÖŠ£¬”ĻA=90”ć£¬AB=3£¬AC=4£¬DĪŖACÖŠµć£¬PĪŖABÉĻµÄ¶Æµć£¬½«PČʵćDÄꏱÕėŠż×Ŗ90”ćµĆµ½P”䣬Į¬CP”䣬ŌņĻ߶ĪCP”äµÄ×īŠ”ÖµĪŖ £® 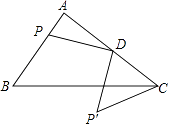
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
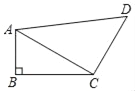
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪABCDÖŠ£¬”ĻB£½90”ć£¬”ĻACB£½30”ć£¬AB£½2£¬CD£½3£¬AD£½5£®
£Ø1£©ĒóÖ¤£ŗAC”ĶCD£»
£Ø2£©ĒóĖıߊĪABCDµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĻĀĶ¼Ź±ÓĆŗŚÉ«µÄÕżĮł±ßŠĪŗĶ°×É«µÄÕż·½ŠĪ°“ÕÕŅ»¶ØµÄ¹ęĀÉ×éŗĻ¶ų³ÉµÄĮ½É«Ķ¼°ø

£Ø1£©µ±ŗŚÉ«µÄÕżĮł±ßŠĪµÄæ鏿ĪŖ1Ź±£¬ÓŠ6æé°×É«µÄÕż·½ŠĪÅäĢ×£»µ±ŗŚÉ«µÄÕżĮł±ßŠĪæ鏿ĪŖ2Ź±£¬ÓŠ11æé°×É«µÄÕż·½ŠĪÅäĢ×£»Ōņµ±ŗŚÉ«µÄÕżĮł±ßŠĪæ鏿ĪŖ3£¬10Ź±£¬·Ö±šŠ“³ö°×É«µÄÕż·½ŠĪÅäĢ×æ鏿£»
£Ø2£©µ±°×É«µÄÕż·½ŠĪæ鏿ĪŖ201Ź±£¬ĒóŗŚÉ«µÄÕżĮł±ßŠĪµÄæ鏿.
£Ø3£©×é³É°×É«µÄÕż·½ŠĪµÄæ鏿ÄÜ·ńĪŖ100£¬Čē¹ūÄÜ£¬Ēó³öŗŚÉ«µÄÕżĮł±ßŠĪµÄæ鏿£¬Čē¹ū²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”°ĪåŅ»ĄĶ¶Æ½Ś“ó³ź±ö£””±£¬Ä³ÉĢ³”Éč¼ĘµÄ“ŁĻś»ī¶ÆČēĻĀ£ŗŌŚŅ»øö²»ĶøĆ÷µÄĻä×ÓĄļ·ÅÓŠ4øöĻąĶ¬µÄŠ”Ēņ£¬ĒņÉĻ·Ö±š±źÓŠ”°0ŌŖ”±”¢”°10ŌŖ”±”¢”°20ŌŖ”±ŗĶ”°50ŌŖ”±µÄ×ÖŃł£®¹ę¶Ø£ŗŌŚ±¾ÉĢ³”Ķ¬Ņ»ČÕÄŚ£¬¹ĖæĶĆæĻū·ŃĀś300ŌŖ£¬¾ĶæÉŅŌŌŚĻä×ÓĄļĻČŗóĆž³öĮ½øöĒņ£ØµŚŅ»“ĪĆž³öŗó²»·Å»Ų£©£®ÉĢ³”øł¾ŻĮ½Š”ĒņĖł±ź½š¶īµÄŗĶ·µ»¹ĻąµČ¼ŪøńµÄ¹ŗĪļČÆ£¬¹ŗĪļČÆæÉŅŌŌŚ±¾ÉĢ³”Ļū·Ń£®Ä³¹ĖæĶøÕŗĆĻū·Ń300ŌŖ£®
£Ø1£©øĆ¹ĖæĶÖĮ¶ąæɵƵ½ŌŖ¹ŗĪļČÆ£»
£Ø2£©ĒėÄćÓĆ»Ź÷דĶ¼»ņĮŠ±ķµÄ·½·Ø£¬Ēó³öøĆ¹ĖæĶĖł»ńµĆ¹ŗĪļČƵĽš¶ī²»µĶÓŚ50ŌŖµÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
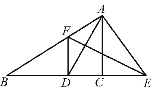
”¾ĢāÄæ”æČēĶ¼,ŌŚ”÷ABCÖŠ,ADŹĒ”ĻBACµÄĘ½·ÖĻß,ADµÄ“¹Ö±Ę½·ÖĻß·Ö±š½»ABÓŚµćF,½»BCµÄŃÓ³¤ĻßÓŚµćE.
ĒóÖ¤:(1)”ĻEAD=”ĻEDA;
(2)DF”ĪAC.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com